Chapter 1: Introduction to John Conway's Genius

I was first introduced to the brilliance of John Conway while working as a teaching assistant at the NSF-sponsored Yale Fractal Geometry Workshops from 2001 to 2007. Among various topics, we delved into cellular automata, which included Conway’s most renowned invention, “The Game of Life.”

Conway was a highly esteemed British mathematician whose influence spanned multiple areas including group theory, number theory, and combinatorial game theory. His playful and innovative approach linked seemingly unrelated fields, garnering him immense admiration in the mathematical community.

In this exploration, we will focus on the intriguing and often perplexing “look-and-say sequence,” first mentioned during the 1977 International Mathematical Olympiad in Belgrave, Yugoslavia. Conway transformed it from a mere curiosity into a significant intellectual achievement in the mid-1980s.

A quick note: in discussing the look-and-say sequence, the terms “sequence” and “string” may vary in usage across different authors. Here, we will use “sequence” to refer to the evolving set of digit strings produced by the algorithm.

Chapter 2: The Look-and-Say Sequence Explained

To define the sequence, we start with the number 1. For clarity, we will omit the usual period at the end: 1

What do you perceive? I see "one one" — meaning one instance of the number 1. We can then translate this observation back into numbers: 11

Now, in this new string, we notice "two ones." Ignoring grammatical plurality, we notate this as: 21

This evolves into: 1211

Before we proceed, why not give the next iteration a try? It’s quite enjoyable! The sequence develops as follows: 1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, 31131211131221, …

You may observe that "3" appears to be the largest digit in the sequence. In fact, no number greater than 3 can emerge from this process after the second term.

As Conway discovered, this seemingly trivial sequence led to remarkably complex outcomes. He first encountered it at a gathering where a student posed a challenge to predict the next term. Initially stumped, once the solution was revealed, he became engrossed. As Conway aptly described: “…and it struck me as the simplest problem with the most intricate solution imaginable.”

The first video, "How the Cosmological Evidence Points to the Existence of God," explores how mathematical patterns can reveal deeper truths.

Chapter 3: Conway’s Constant and Its Implications

The length of the output increases exponentially according to a ratio known as Conway's constant ?, which is approximately: ? ≈ 1.3035772690342963912…

It’s fascinating that such an ostensibly arbitrary sequence could grow in a predictable manner. Conway demonstrated that ? is an algebraic number, specifically the unique positive real root of a degree-71 polynomial.

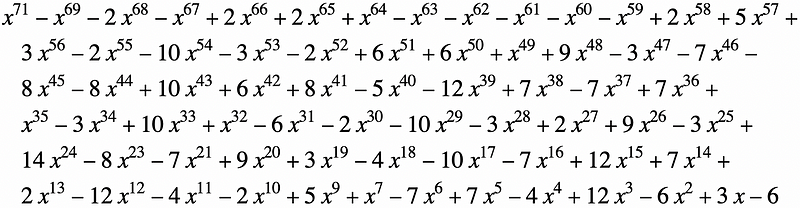
In his own words, Conway remarked: “To me, ? is the most complicated algebraic number derived from the simplest source imaginable.”

The second video, "Does the Fine Tuning of the Universe Demonstrate the Existence of God?" further investigates how mathematical concepts can intersect with profound philosophical questions.

Chapter 4: The Intersection of Mathematics and Chemistry

In 1986, Conway published a paper titled "The Weird and Wonderful Chemistry of Audioactive Decay." This work delves into the peculiarities of the sequence, revealing that any finite string, starting from the eighth term, will split into distinct, independent strings. Remarkably, there are exactly 92 of these foundational strings, which he named after elements from the periodic table.

To illustrate, consider the eighth term: 1113213211

This can be split as follows: 11132.13211

From here, the strings on either side of the split evolve independently.

To understand this concept better, refer to the table below, which shows how these strings progress without influencing one another.

Conway's Cosmological Theorem suggests that any initial number in the look-and-say sequence will ultimately form a compound made up of these fundamental elements in a finite time frame.

Here are some elements from Conway’s "Periodic Table":

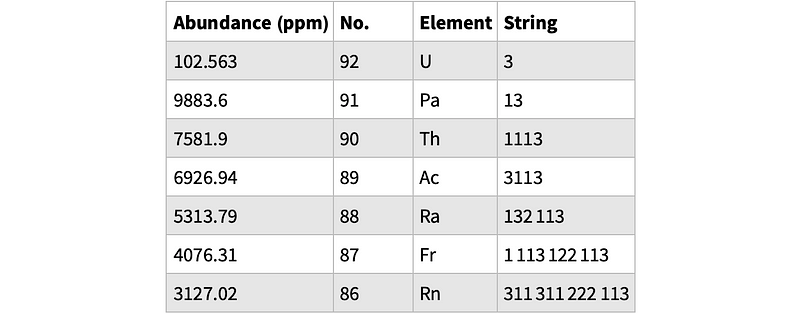
In a simplified example, Term 9 from the earlier table splits into: Element 71 (Lutetium): 311312, and Element 49 (Indium): 11131221, leading to: 31131211131221 = Lu.In

However, the complexity escalates quickly. Conway noted that proving the Cosmological Theorem is remarkably challenging, yet his insights laid the groundwork for further exploration in this fascinating intersection of mathematics and chemistry.

Thank you for reading! If you found this piece insightful, please consider hitting the “Applause” icon. You can also subscribe for my latest content delivered directly to your inbox.