Gravitational Fields

Einstein's formulation of gravity, now widely embraced, characterizes it as a field. This indicates that gravity is a spatial quantity that varies at each coordinate point. In everyday language, references to fields are uncommon; we tend to simplify measurements by generalizing them over larger areas, such as discussing “room temperature.” However, in strict terms, a field exhibits different values at each minuscule point, as illustrated in Figure 1, which depicts a two-dimensional field.

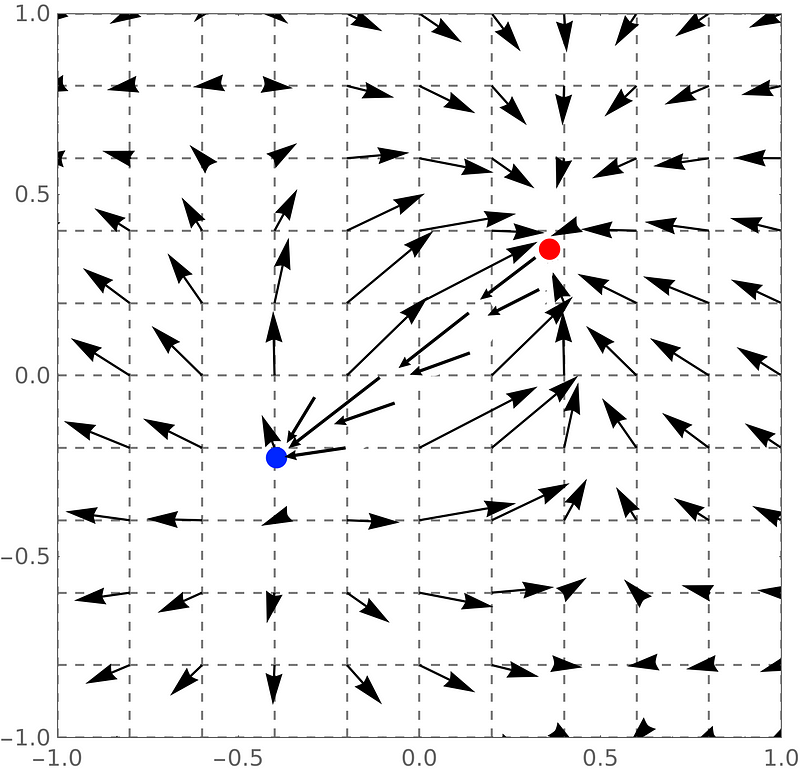
The labels in Figure 1 are omitted to signify that these are spatial positions, applicable in various coordinate systems, such as number line, polar, cylindrical, and Cartesian coordinates. Einstein utilized such a system to articulate the presence of gravity within the coordinates of x, y, z, and time, which he collectively termed spacetime. The culmination of Einstein's efforts led to what we now refer to as Einstein’s Field Equations, typically presented in tensor form:

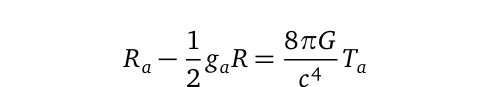
Here, R? represents Ricci's tensor, R is its trace, g? denotes the spacetime metric, and T? is the matter energy–momentum tensor, which includes the cosmological constant. G is Newton's universal gravitational constant, while c is the speed of light in a vacuum. Notably, these equations are plural, indicating they can be broken down into multiple equations, specifically ten. One method of decomposition is through Taylor series expansion, named after British mathematician Brook Taylor, who introduced it in 1715.

Einstein’s field equations are recognized for their complexity and computational demands. Interestingly, Einstein himself doubted that an exact solution would ever be found, eventually leading to only approximate solutions. The primary source of errors in his equations stems from the Taylor series expansion methodology, which allows for error propagation based on the number of terms utilized. Thus, it is fair to assert that Einstein's solutions were also constrained by the limited computational resources of his era¹.

Nevertheless, there have been various attempts to solve these equations, with the first exact solution attributed to Karl Schwarzschild, a German physicist, astronomer, and World War I veteran, in 1915—the same year Einstein published the field equations. The solutions to Einstein’s field equations are termed metrics, and the Schwarzschild solution is also known as the Schwarzschild metric. This solution leads to the concept of the Schwarzschild radius, r?, which describes the event horizon of a non-rotating black hole. The mathematical representation is given by:

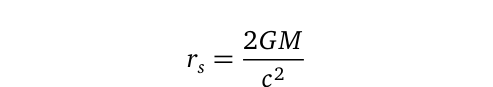
Over time, other significant solutions to Einstein’s field equations have emerged, such as the Reissner–Nordström, Kerr, and Kerr-Newman metrics, each corresponding to different types of black holes. In summary, while describing gravity as a field does not elucidate its source, it does clarify where gravity manifests in our universe—within the field.

Gravity as a Curvature in Space

Another perspective on gravity is viewing it as a curvature within the spacetime fabric created by massive objects. This interpretation is widely accepted, yet it often falls short of explaining the source of gravity itself and can be somewhat misleading. The notion of gravity as a force that bends spacetime can confuse readers, as it fails to address what causes the attraction noted by Isaac Newton, particularly when comparing two objects of differing masses situated at the same level.

The synthesis of both models leads to an understanding where Newtonian gravity is seen as a pulling force between masses at a uniform level, while Einstein’s framework quantifies gravity in terms of the “depression” or vortex created by a massive object in the spacetime matrix. Consequently, lighter masses tend to gravitate towards the created vortex.

Spacetime-f: The Extension of Spacetime

This section aims to demonstrate that for each coordinate x, y, z, t referenced in Einstein’s gravitational field description as the dependent variable, an additional frequency term exists, exhibiting wave-like characteristics.

It is widely accepted that the universe comprises pure frequencies; however, this idea remains largely philosophical when considering large-scale objects. Notable methods exist for estimating wave properties of elementary particles, such as de Broglie and Compton wavelengths. Compton’s approach was particularly groundbreaking, enabling the precise determination of the rest mass of particles that would otherwise be challenging to measure. According to Compton scattering, a particle's wavelength corresponds to that of a photon with equivalent energy to its mass, represented as follows:

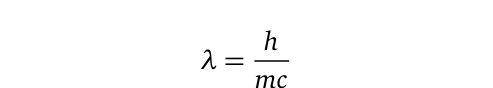
Where h is Planck’s constant, and c denotes the speed of light in a vacuum. However, it’s essential to note that this equation is applicable only to individual, homogeneous particles, excluding composites. Thus, it may yield trivial outcomes when applied to significantly large bodies like planets.

This compels us to derive an equivalent of the Compton formula for larger objects, allowing us to associate any mass with a wave property, such as frequency or wavelength. The solution lies in utilizing an exact answer to Einstein’s field equations. For any object, regardless of its size, the equivalent Compton wavelength can be expressed as:

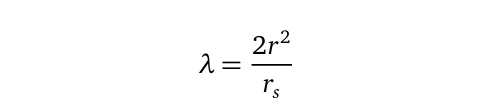
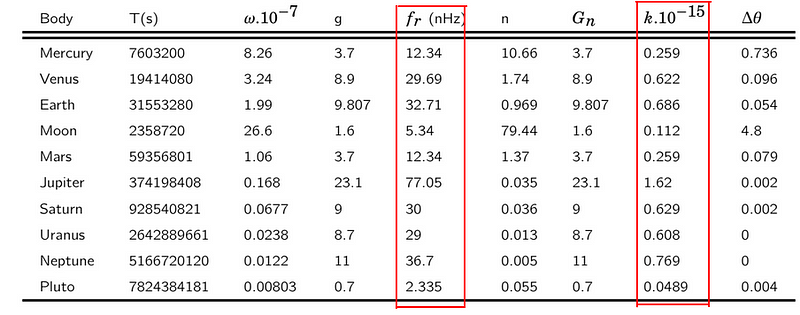
Here, r? is the Schwarzschild radius. The wave numbers for the specified wavelength can also be derived through the reciprocal relation k=1/?. A range of nearby planetary bodies has been analyzed using this methodology, as shown in Table 1.

Transforming massive objects into their single-particle Compton wavelengths allows us to obtain their associated radio frequencies through the classical electromagnetic wave equation f=c/?. This presents an opportunity to estimate Newtonian gravitational potential g as follows:

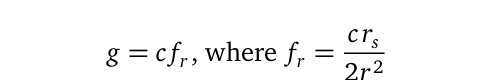
This method applies universally to celestial bodies, including planets, moons, neutron stars, and black holes, because it can revert to our conventional understanding of Newtonian gravity. This is accomplished through the following steps:

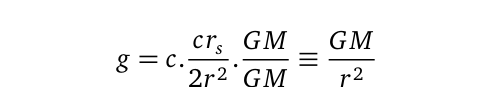
Where M signifies the mass of the object in question. The second advantage of this approach is the ability to characterize celestial bodies from planets to black holes, including their identification. This can be achieved through any radar mapping method, from which gravitational potential g can be derived using the previous equation, and the radii can be calculated as follows:

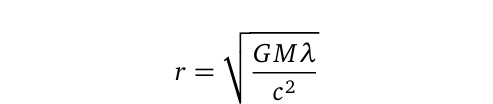
The minimum value that r can take in Eq. (4) is r?, indicating that an object with a radius equal to or less than its Schwarzschild radius qualifies as a black hole. For such a system, Eq. (4) can be simplified to ? = 2r?. This means properties of a black hole, including mass, energy density, and Schwarzschild radius, can be estimated once the relevant radio frequencies are obtained. For Schwarzschild black holes, mass and gravitational radii can be estimated as follows:

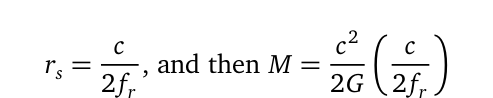
Stars like our sun gradually lose energy—termed nucleosynthetic power—albeit in minuscule amounts, ultimately leading to the formation of a black hole at their core. If we were to model such an event using this methodology, we would allow the wavelength to recede by an amount ?h=?-r at any given moment. The resulting metric solution would then be expressed as:

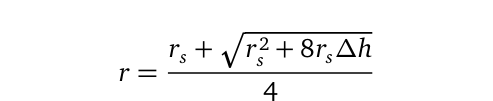
This indicates that an object may not become a black hole as long as the difference ?h between its radius and its corresponding wavelength exceeds r?. The only challenge in determining wave frequencies related to gravitational fields is the potential lack of accurate detection tools, given that these frequencies are ultra low (ULF) and situated at the extremes of the electromagnetic spectrum.

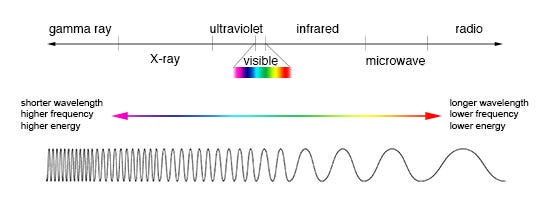
The frequencies we seek are located far right in Figure 3, indicating that they possess long wavelengths and low energy, on the order of nanoHertz. For Earth, this frequency is 32.71 nanoHertz, Jupiter has a frequency of 77.05 nanoHertz, while Pluto’s frequency is 2.335 nanoHertz.

As a side note, the universal gravitational constant is not as universal as previously thought; it is, in fact, a constant relative to the planet where calculations are made. This implies that the constant 6.6743E-11 is applicable only to Earth. In a stricter sense, it varies for each massive object, being proportional to its extent r, mass M, and the proportionality constant is the surrounding frequencies discussed herein.

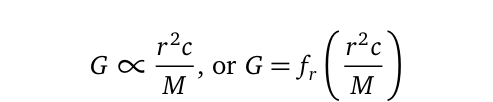
This discussion underscores why attempts to apply general relativistic calculations to quantum mechanics often yield disparate results; in such cases, G is on the order of 10E-54.

Conclusion

There is substantial evidence to support the notion that every coordinate in a gravitational field, as described by Einstein in terms of spacetime, can be correlated with wave properties. This correlation allows for further characterization of the gravitational field. Specifically, massive objects in a gravitational field emit a wavelength that is considerably larger than their own radii.

These wavelengths correspond to radio frequencies that, if accurately mapped, can provide insights into various properties related to the gravitational fields encompassing these objects. This methodology is termed spacetime-f, as it introduces a response frequency variable f?, quantifiable for each coordinate x, y, z, and t. Thus, mass is no longer the sole means of detecting curvatures in spacetime; the concept of radio frequencies serves as an additional candidate for space exploration, provided they are within our electromagnetic spectrum.

A thorough understanding and implementation of these methods could pave the way for advancements in technologies such as sound navigation and detection ranging (sonar, sodar, and radar) on micro-scales, as well as potential developments in anti-gravity technologies.

References

¹ Miller, Mark. “Accuracy requirements for the calculation of gravitational waveforms from coalescing compact binaries in numerical relativity.” Physical Review D 71.10 (2005): 104016.

² https://science.nasa.gov/science-news/science-at-nasa/2005/16nov_gpb

³ https://www.nasa.gov/multimedia/guidelines/index.html