Mastering Recursion and Dynamic Programming for Optimization
Written on
Understanding Recursion and Dynamic Programming
When faced with the challenge of determining the fewest coins needed to reach a specific amount using coins of varying denominations, the problem becomes one of optimization. For instance, if you're given coins of 1 cent, 5 cents, and 10 cents, and tasked with making 18 cents, how would you approach it?
This scenario illustrates an optimization problem where the goal is to minimize the number of coins used to reach a designated total. The solution requires a recursive approach, evaluating whether including each coin denomination contributes to achieving the target amount.
However, recursion can introduce significant overhead due to the repeated calls to the same functions, which may lead to exponential or logarithmic time complexity, depending on the number of recursive calls and the complexity of operations involved. Consequently, this can lead to longer execution times.
Is there an effective strategy to enhance execution efficiency?
Dynamic programming provides a solution to the time complexity challenge by decomposing the recursive problem into simpler sub-problems.
Dynamic programming is a mathematical optimization strategy and programming methodology that allows for the discovery of optimal solutions to complex recursive issues by breaking them down into manageable sub-problems, solving each sub-problem once, and storing the results.
Which Problems Can Dynamic Programming Address?
Dynamic programming is applicable when two essential characteristics are present:
- Optimal Substructure: The optimal solution to the entire problem can be derived from the optimal solutions of its sub-problems, adhering to the principle of optimality. Essentially, this means the problem can be subdivided into smaller, manageable components.
- Overlapping Sub-Problems: During the recursive process, the same sub-problems are solved multiple times.
For example, calculating the Fibonacci number for 6 demonstrates dynamic programming in action.
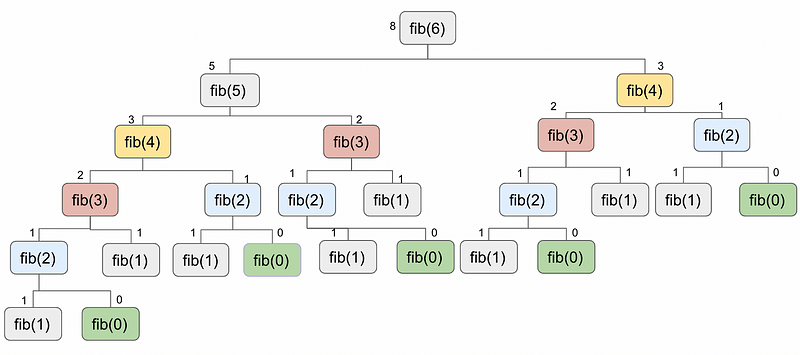
As illustrated, the recursive function repeats multiple times, leading to inefficiencies, especially when calculating larger Fibonacci numbers like 100. This scenario showcases both necessary dynamic programming traits: optimal substructure and overlapping sub-problems.
In the example above, the Fibonacci(2) function is called five times, highlighting the overlapping sub-problems characteristic.
Dynamic programming techniques are adept at providing optimal solutions to recursive dilemmas by solving each sub-problem just once and retaining the outcomes.
Dynamic Programming Approaches
Dynamic programming can be implemented through two main strategies:
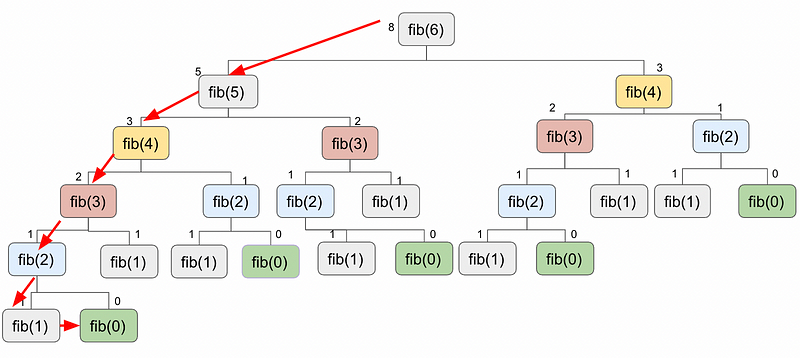
1. Top-Down Approach (Memoization):
This method involves breaking the problem into sub-problems, starting from the top of the recursion tree and moving downwards. Results are cached, so if a sub-problem has already been solved, the cached result is utilized.
This approach resembles traditional recursion but distinguishes itself by caching sub-problem results, which are then reused in subsequent recursive calls. The cache may be structured using an array or a hash table, allowing the evaluation of only the necessary sub-problems to resolve the larger issue.
2. Bottom-Up Approach (Tabulation):
In this strategy, the problem is reorganized, tackling the smallest sub-problems first before progressing to larger issues, thereby avoiding the pitfalls of recursion.
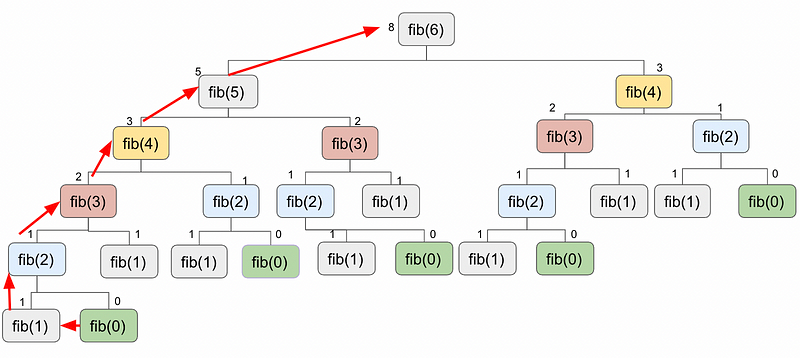
This method sequentially resolves sub-problems, moving from the bottom to the top, while storing results in a table referred to as tabulation. In this approach, all sub-problems are addressed, regardless of their contribution to the final solution.
While memoization is simpler to implement, it can be slower due to its reliance on recursion, which carries the risk of stack overflow if the recursion tree grows too deep.
Practical Implementation in Python
Below is a Python implementation showcasing recursion, memoization, and tabulation techniques.

The following code snippet addresses the coin minimization problem through dynamic programming:
INF = 100000
def coin_change_modified(denomination, amount, no_of_coins):
No_of_ways = [0] * (amount + 1)
coins_for_amount = [0] * (amount + 1)
for j in range(1, amount + 1):
minimum = INF
coin = 0
for i in range(1, no_of_coins + 1):
if j >= denomination[i]:
minimum = min(minimum, 1 + No_of_ways[j - denomination[i]])
coin = i
No_of_ways[j] = minimum
coins_for_amount[j] = coin
l = amount
while l > 0:
print(denomination[coins_for_amount[l]])
l = l - denomination[coins_for_amount[l]]
return No_of_ways[amount]
if __name__ == '__main__':
# array starting from 1, element at index 0 is fake
d = [0, 1, 2, 5, 10]
coin_change_modified(d, 9, 4) # to make 5. Number of denominations = 3
As the saying goes, "Those who cannot remember the past are condemned to repeat it" — a principle that resonates with the essence of dynamic programming.
The first video title is Introduction to Recursion - Learn In The Best Way - YouTube, which provides a foundational overview of recursion concepts.
The second video title is 5 Simple Steps for Solving Any Recursive Problem - YouTube, which outlines effective strategies for tackling recursive challenges.