Understanding Shortest Paths in Spacetime: A Complex Journey
Written on
The final installment of my exploration into "The Pythagorean Legacy" will delve into the concepts of geodesics within Riemannian and pseudo-Riemannian geometry. In these geometries, distance and angles arise from position-dependent quadratic forms on the tangent space of a suitably differentiable manifold, essentially rooted in local interpretations of Pythagoras's Theorem.

Defining what constitutes “angle” and “direction” can be quite perplexing. The Pythagorean concepts resonate universally, extending beyond mathematics into social paradigms—expressions like "the path of least resistance" are prevalent in English and German discussions.
The concept of the shortest or extremal path is inherently intuitive; most mammals seem to grasp it instinctively. However, in the realm of geometry, this notion presents significant challenges. An extremal path in geometry—whether maximum, minimum, or an infimum/supremum—is referred to as a geodesic, a term derived from the Greek words gaia (earth) and daiein (to divide), reflecting the historical context of surveying.
In 1828, the renowned mathematician Carl Friedrich Gauß was tasked with surveying the land of Hannover on behalf of his British rulers. While his methods were not entirely precise, they marked a significant advancement in surveying techniques. Gauß’s work laid the groundwork for his groundbreaking ideas in non-Euclidean geometry, developed through his meticulous use of orthogonal curvilinear coordinates and complex analysis techniques.
Gauß was cautious about publishing his findings, preferring to wait until he felt he had exhausted all possibilities. Consequently, while János Bolyai and Nikolai Lobachevsky are credited with the initial publications on non-Euclidean geometry, Gauß held a more comprehensive vision of the subject.
Gauß entrusted his PhD student, Bernhard Riemann, with further developing these ideas. Whether this decision stemmed from generosity or a desire for protection against criticism remains a topic of debate.
At the heart of Riemannian and pseudo-Riemannian geometry lies the concept of a geodesic—the shortest route connecting two points within a manifold. In a pseudo-Riemannian manifold, the metric is not positively definite, reflecting its more complex (non-Euclidean) nature.
Though the idea of a geodesic may initially seem straightforward, it harbors peculiarities that require careful consideration.
Singular Hamiltonians for (Pseudo) Riemannian Geodesics
Attempting to apply a Hamiltonian approach to determine a shortest path can lead to the unsatisfactory conclusion that 0=0. This unexpected outcome necessitates a deeper understanding of the issue at hand. The shortest path, formulated as an “action integral” in the context of Lagrangian calculus, is not as precisely defined as one might assume, complicating the Hamiltonian approach.
To visualize this, consider a car journey from point A to point B. Along the way, you have the freedom to stop for a romantic encounter or a delightful treat, yet you still arrive having traveled the shortest distance.

Regardless of the speed or time profile chosen along your route, the path remains the same.
A Lagrangian Perspective
Here’s the Lagrangian we need to optimize using the Euler-Lagrange equation:
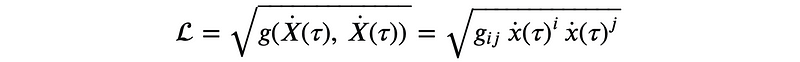
In this equation, g signifies the metric tensor acting on the tangent space, while d*X*/d*t represents the velocity vector. The contravariant components of this vector are given in a simplified format.
We can express the total action integral as the complete length of the curve traced out as X(?) varies from 0 to 1. Moreover, if we transform the path parameter, we can maintain the same path while altering the speed-time profile, thereby introducing additional degrees of freedom.
Examining the Hamiltonian Approach
When transitioning to a Hamiltonian framework, a crucial requirement is that the Lagrangian must be a strictly convex function of the velocities; otherwise, the Legendre transform may fail. The conjugate momentum derived from our previous integrand remains unchanged by any proportional scaling of the velocities.
To illustrate, if we pursue the Hamiltonian without the square root, we may inadvertently bypass the complications it introduces. Remarkably, the Cauchy-Schwarz inequality can aid in navigating these challenges, leading to elegant solutions.
Conclusion
In essence, our exploration of geodesics within Riemannian and pseudo-Riemannian manifolds reveals not only the shortest paths but also presents an affine parameterization of these trajectories. In the context of relativity, this concept is particularly significant, where observers experience their proper time uniformly, allowing us to focus on the physical path characterized by constant speed.
Understanding these complex ideas enriches our comprehension of the universe's underlying geometry, revealing the intricate dance between mathematics and physical reality.
