The strong nuclear force reveals why only eight gluons exist.

One of the most intriguing aspects of our universe is the strong nuclear force. Within each proton or neutron, there are three quarks, each assigned a distinct color. These colors combine to form a colorless state, which appears to be a fundamental requirement of the universe. One can have either three quarks, three antiquarks (with their respective anticolors), or a mix of quarks and antiquarks that balance each other out. Recent discoveries of tetraquarks (two quarks and two antiquarks) and pentaquarks (four quarks and one antiquark) also support the creation of colorless quantum states.

Despite having three colors and three anticolors in nature, the particles that facilitate the strong force—gluons—exist in only eight varieties. One might assume that every conceivable color-anticolor pairing would be valid, leading to a total of nine gluons, but the universe operates under different principles. Here, we explore the fascinating physics behind the limitation of gluons to just eight.

In the realm of physics, only a handful of fundamental forces exist, each with its own set of rules. Gravitational force only involves one type of charge—mass/energy—that is always attractive. There’s no cap on how much mass/energy one can possess; the worst outcome is the formation of a black hole, which still adheres to gravitational theory. Every energy quantum, regardless of whether it has mass (like an electron) or not (like a photon), warps space-time, creating what we perceive as gravity. If gravity is indeed quantum in nature, a single quantum particle, the graviton, is sufficient to convey gravitational force.

Electromagnetism, another fundamental force observable on larger scales, offers a bit more complexity. It has two types of charge: positive and negative electric charges. Like charges repel each other, while opposite charges attract. Although the principles of electromagnetism differ significantly from those of gravity, its framework remains relatively straightforward, similar to that of gravity. Free charges can exist in any quantity, and just one particle, the photon, is needed to mediate all electromagnetic interactions.

When we examine the strong nuclear force, however, the rules diverge significantly. Instead of a single charge (as in gravity) or two (as in electromagnetism), the strong force operates with three fundamental charges known as colors. The behavior of these colors follows unique rules that differ from other forces:

• Net charge cannot exist; only "colorless" states are permissible.
• A color paired with its anticolor results in a colorless state; all three unique colors (or anticolors) combined are also colorless.
• Each quark carries a net color charge, while each antiquark is associated with an anticolor.
• The only other Standard Model particle that possesses color is the gluon, which facilitates the exchange between quarks, resulting in bound states.

These intricate rules, while distinct from gravity and electromagnetism, enhance our understanding of how particles like protons and neutrons are held together.

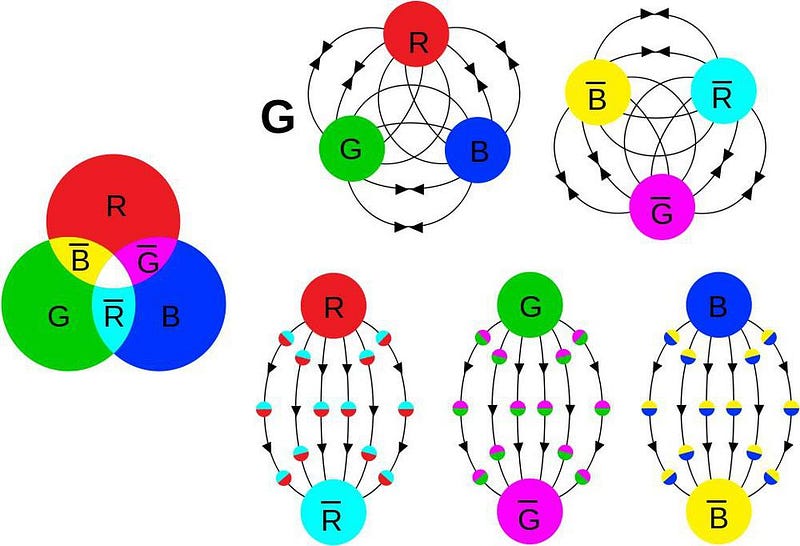
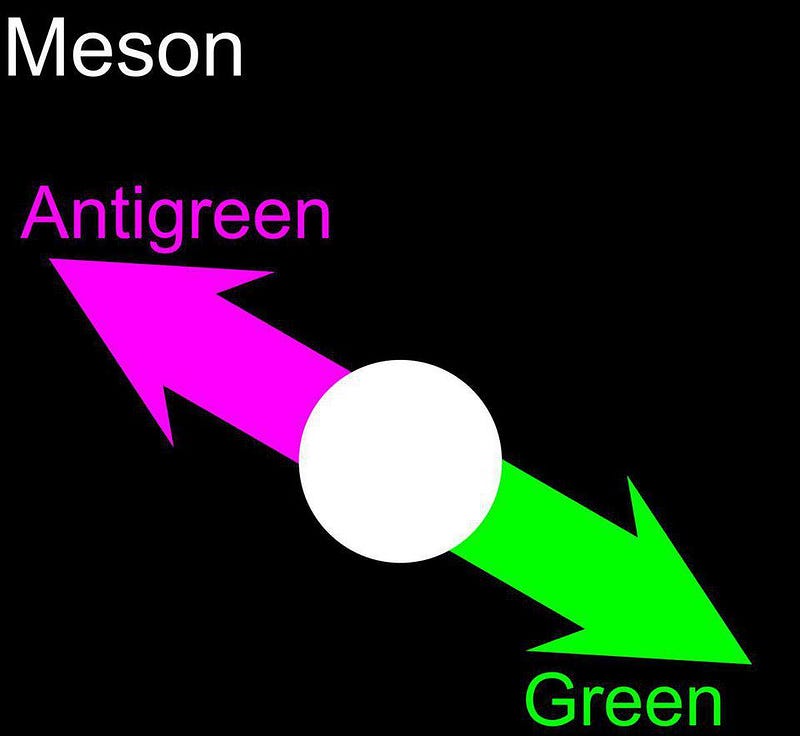
Firstly, protons and neutrons, alongside other similar particles termed baryons, must consist of three quarks, each displaying a different color. For every baryon, there exists an antiparticle counterpart made up of three antiquarks, each carrying a different anticolor. Every possible configuration at any given moment must be colorless, necessitating one red, one green, and one blue quark, along with one cyan (anti-red), one magenta (anti-green), and one yellow (anti-blue) antiquark.

As with all particles governed by quantum field theory, the strong nuclear force operates via particle exchange. However, the structure of the strong force's theory is notably more complex than that of gravity or electromagnetism. While gravity does not alter the mass/energy of interacting particles, and electromagnetism does not modify the electric charge of attracting or repelling particles, the colors (or anticolors) of quarks (or antiquarks) shift with every occurrence of the strong nuclear force.

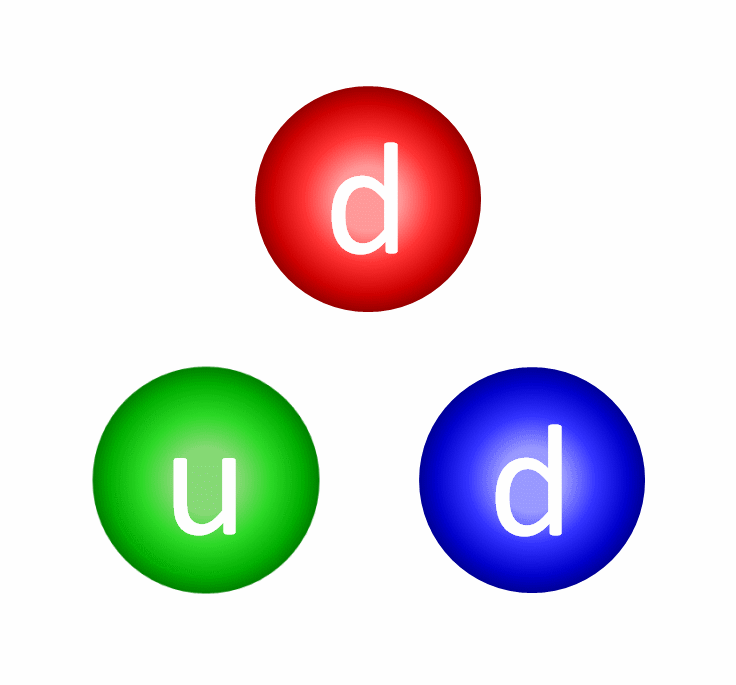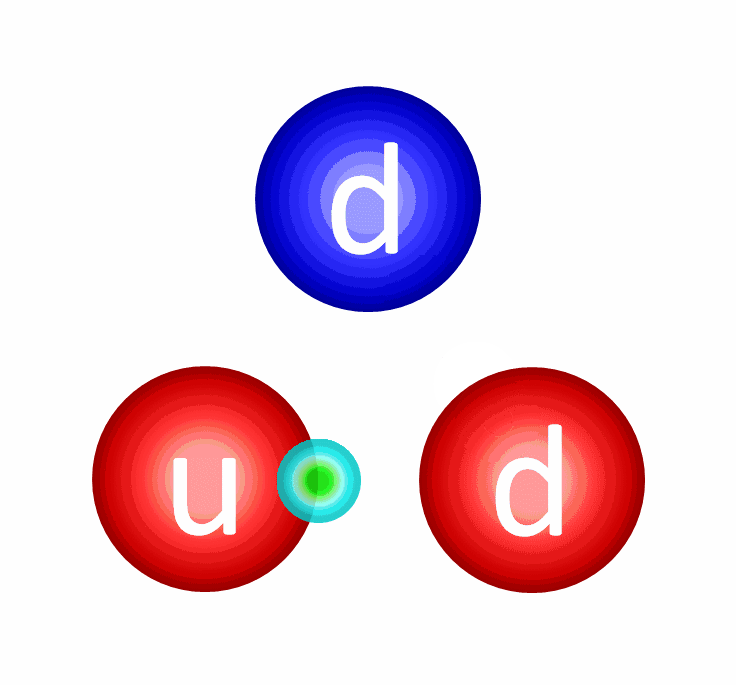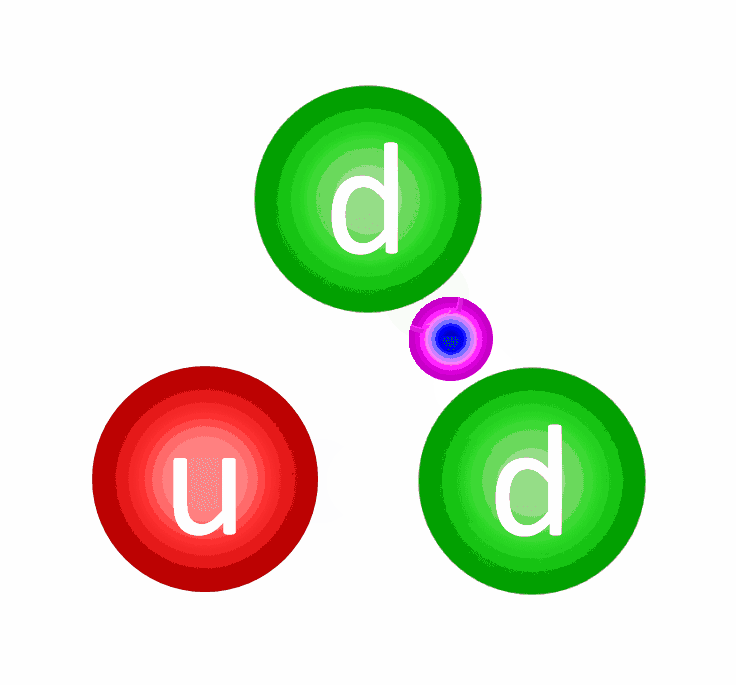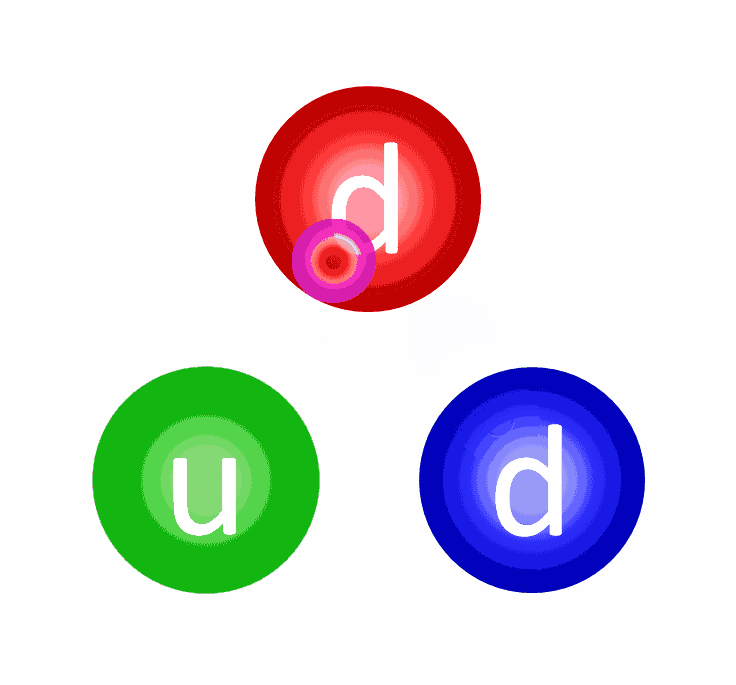
This exchange can be visualized through gluons. Each gluon is emitted by one quark (or antiquark) and absorbed by another quark (or antiquark), mirroring the process of electromagnetism where each photon is emitted by one charged particle and received by another. The photon serves as the force carrier for electromagnetic interactions, while gluons are the particles responsible for the strong nuclear force.

At first glance, one might assume there are nine gluons, corresponding to every conceivable color-anticolor pairing. This assumption is grounded in simple logic: three colors and three anticolors imply nine potential gluons. Visualizing the interactions inside a proton, one could see:

• A quark emits a gluon, altering its color.
• That gluon is then absorbed by another quark, changing its color.

This framework provides a clear picture of six possible gluon interactions.

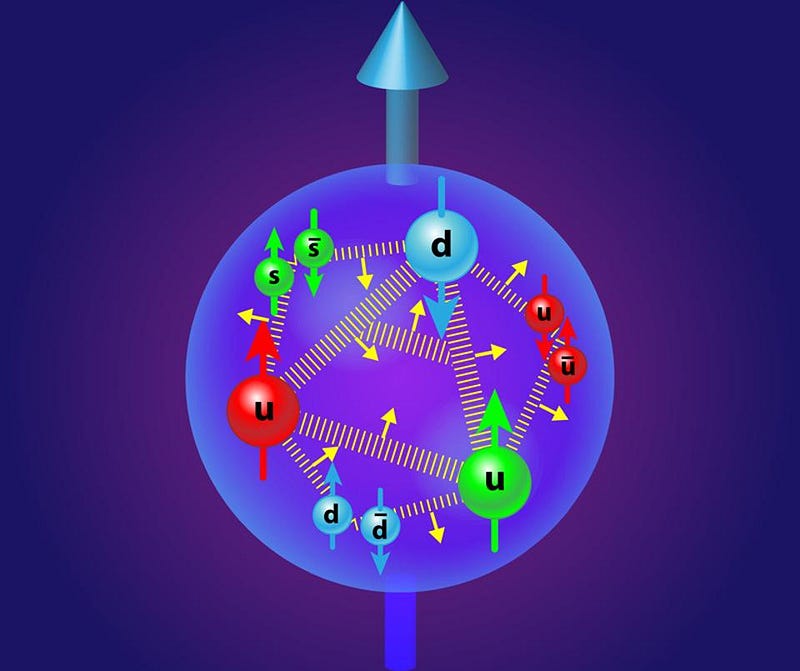
If we imagine three gluons within a proton—one red, one green, and one blue, which together yield a colorless state—then the following six gluon exchanges could occur:

1. The red quark may emit a red-antiblue gluon, turning it blue while converting the blue quark to red.
2. Alternatively, it could emit a red-antigreen gluon, changing it to green while the green quark becomes red.
3. The blue quark might emit a blue-antired gluon, turning it red while the red quark turns blue.
4. Or it could emit a blue-antigreen gluon, shifting to green while the green quark turns blue.
5. The green quark could emit a green-antired gluon, resulting in a red quark that turns green.
6. Lastly, it might emit a green-antiblue gluon, converting to blue while the blue quark turns green.

These account for the six straightforward gluons. But what about the remaining ones? Wouldn't one expect to also find a red-antired, a green-antigreen, and a blue-antiblue gluon?

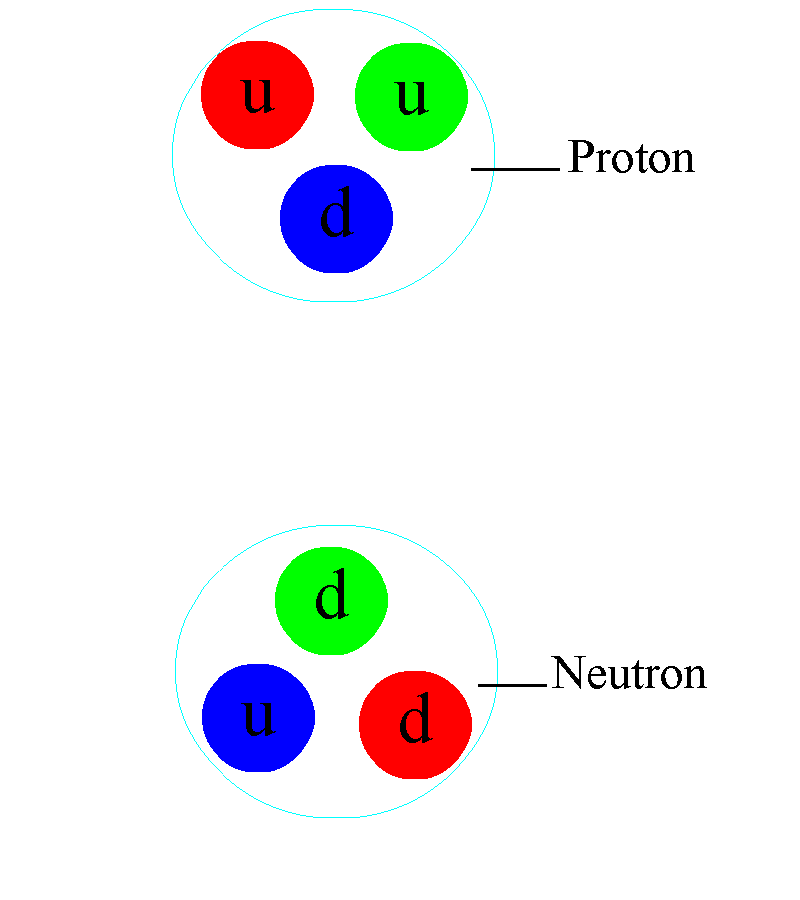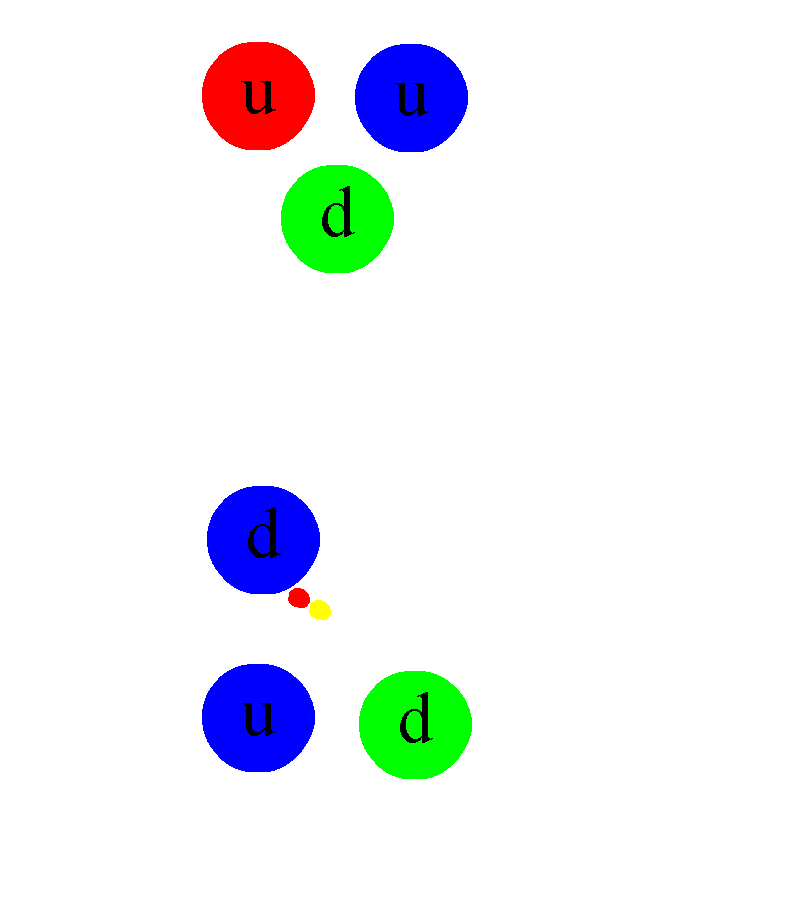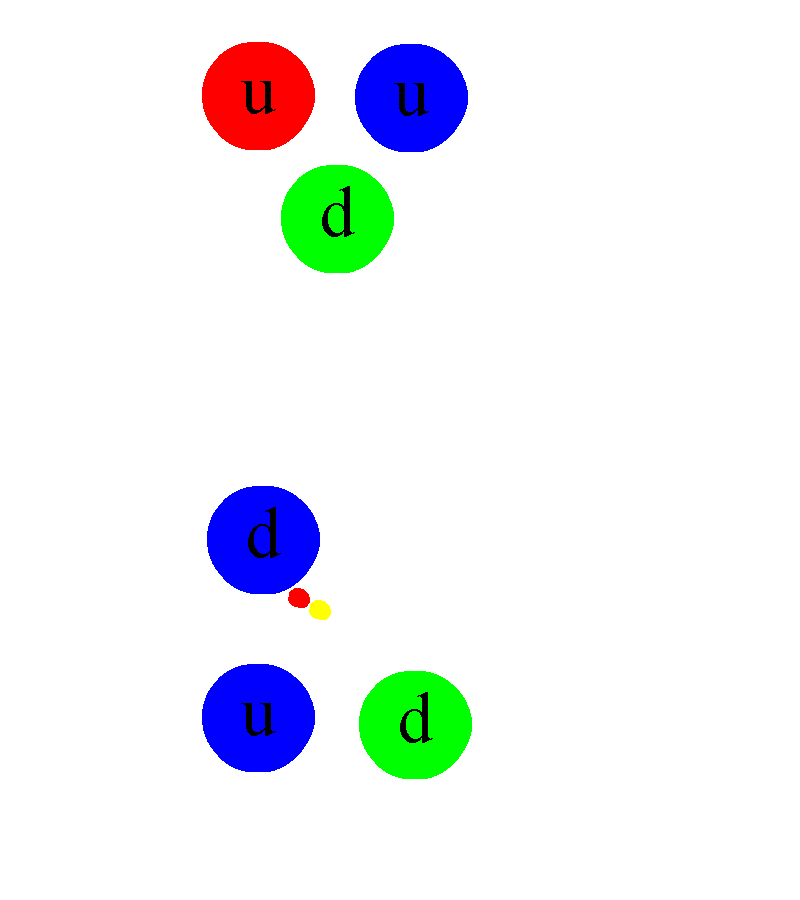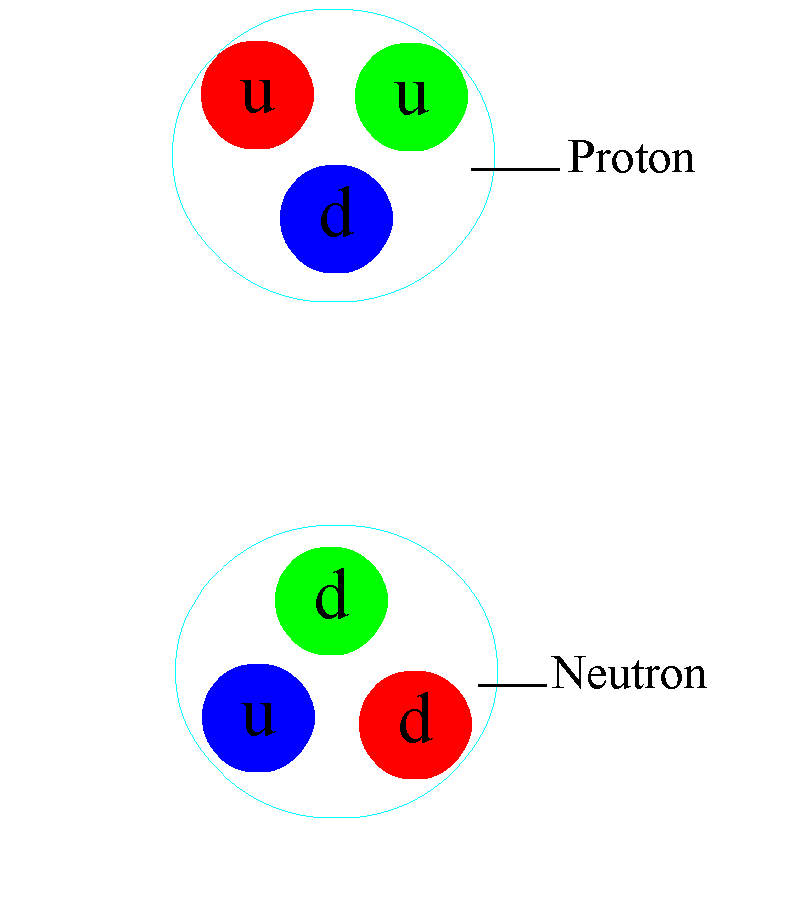
Unfortunately, the answer is no. Consider a scenario where you had a red-antired gluon. A red quark could emit this gluon, remaining red. But which quark would absorb it? The green quark cannot, as there’s no “antigreen” part to neutralize it and revert it to a colorless state. The same applies to the blue quark, which lacks an “antiblue” component.

Does this imply that only six gluons exist, excluding the others?

Not exactly. While a pure "red-antired" or "green-antigreen" cannot occur, a mixed state that includes red-antired, green-antigreen, and blue-antiblue can be formed. Quantum physics dictates that particles (or combinations thereof) with identical quantum states inevitably mix together. For instance, the neutral pion is a blend of up-antiup and down-antidown quarks, and the other permitted gluons are mixtures of red-antired, green-antigreen, and blue-antiblue.

However, there aren’t three such gluons. The key reason lies in the specific characteristics of the strong force, which imposes an additional constraint. For each color-anticolor combination present, a negative color-anticolor combination from a different color is required to form a genuine gluon.

To illustrate, if you desire a gluon with both red-antired and blue-antiblue traits (arbitrary color choices), the required combination would be:

[(text{red-antired}) - (text{blue-antiblue})/2]

This incorporates a negative sign. Now, if you wish to define another gluon independent of the first, it could look like this:

[(text{red-antired}) + (text{blue-antiblue}) - 2*(text{green-antigreen})/6]

Can a third independent combination be created?

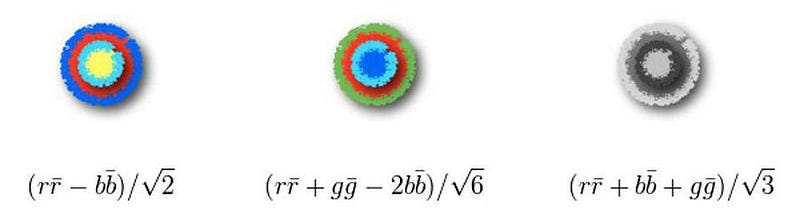
Yes, but it would violate the previously mentioned rule. You could construct a third gluon in the following manner:

[(text{red-antired}) + (text{blue-antiblue}) + (text{green-antigreen})/3]

This would yield an independent combination of the prior two. If this were permissible, we’d have a ninth gluon. However, as anticipated, this is not feasible. All components of color-anticolor are positive, and the absence of a negative combination means that this hypothetical gluon isn’t physical. For any three color-anticolor combinations, only two independent configurations with negative signs can exist; the third will invariably be positive.

In terms of group theory, the gluon matrix is traceless, differentiating the unitary group U(3) from the special unitary group SU(3). Had the strong force been governed by U(3) instead of SU(3), an additional, massless, completely colorless gluon would exist, behaving like a second photon. However, our universe contains only one type of photon, confirming experimentally that only eight gluons are present.

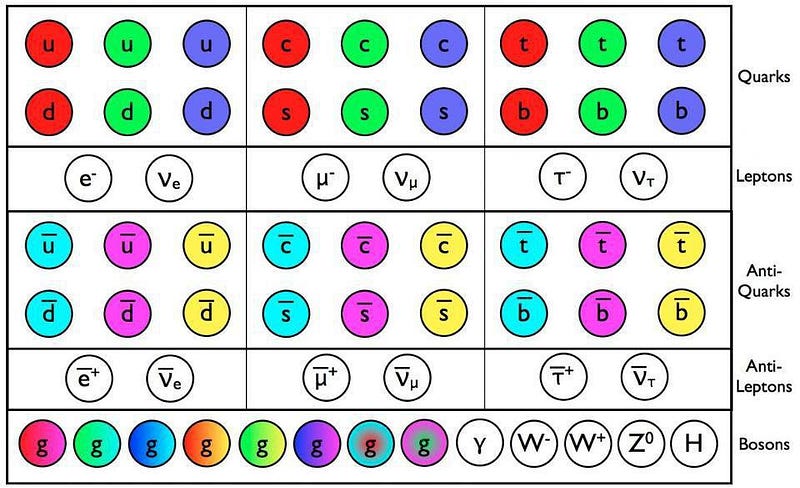
With three colors and three anticolors for quarks and antiquarks, it is the interplay of color-anticolor particles that facilitates the strong nuclear force among them: the gluons. Six gluons are straightforward, featuring color-anticolor combinations with distinct anticolors, while the remaining two are combinations of colors-anticolors mixed with a negative sign. The only other allowable combination is colorless, which fails to satisfy the criteria for a physical particle. Consequently, only eight gluons exist.

It is truly remarkable how well the mathematics of group theory describes the Standard Model, with the strong force aligning perfectly with its predictions. Unlike gravity (featuring solely one type of attractive charge) or electromagnetism (which possesses both positive and negative charges), the properties of color charge exhibit much greater intricacy, yet are entirely comprehensible. With merely eight gluons, we can bind every physically conceivable combination of quarks and antiquarks throughout the universe.

Starts With A Bang is authored by Ethan Siegel, Ph.D., the writer of Beyond The Galaxy and Treknology: The Science of Star Trek from Tricorders to Warp Drive.