A Circle as a Unique Ellipse

You might recognize the equation x² + y² = r² as representing a circle. Specifically, when r = 1, it describes a unit circle centered at the Origin. Consider a line segment drawn from the Origin, O, to any point on the circle, A. This segment serves as the hypotenuse of a right triangle, with the lengths of the legs correlating with the x and y coordinates of point A, which forms a vertex of the triangle.

The equation x² + y² = r² mirrors the Pythagorean Theorem because it indeed reflects the relationship between the sides of right triangles with a hypotenuse of length r.

This definition may not seem as straightforward as stating that a circle is the set of points equidistant from a center, but it allows for broader generalizations. For instance:

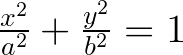
By introducing parameters a and b, we can manipulate the circle's dimensions in either direction. When a = b = 1, we revert to a circle. However, if we set b = 2, effectively scaling y by a factor of 2, we achieve a modified shape.

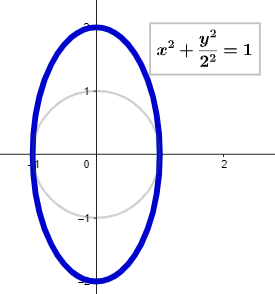
Typically, we express the coordinates of a point A on the circle using parametric equations:

Here, the angle ? acts as our parameter, often associated with the arc length it subtends. However, it’s beneficial to redefine this angle in terms of twice the area of the sector formed by the radius, the x-axis, and the arc. A quarter turn corresponds to an area of ¼?, making the angle equivalent to ½?.

In principle, we could establish various forms of elliptical trigonometry by redefining sine and cosine functions according to the new scale. But what occurs when we distort the circle significantly enough to turn it inside out?

A Hyperbola as a Circle with an Imaginary Radius

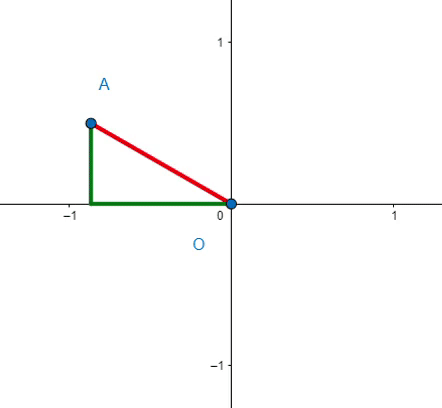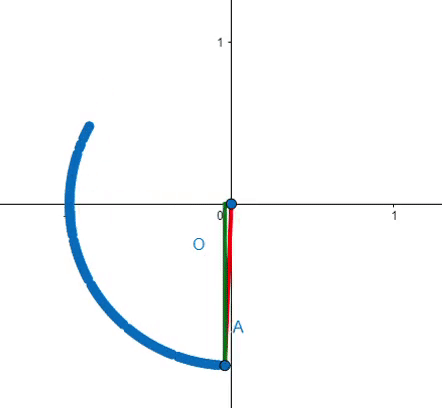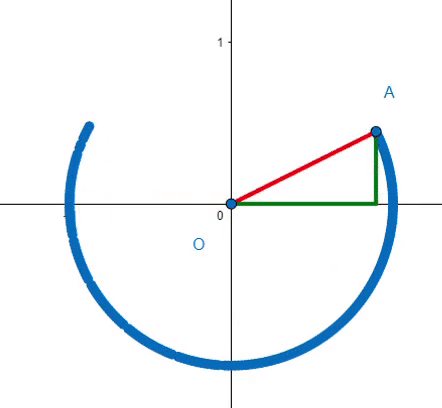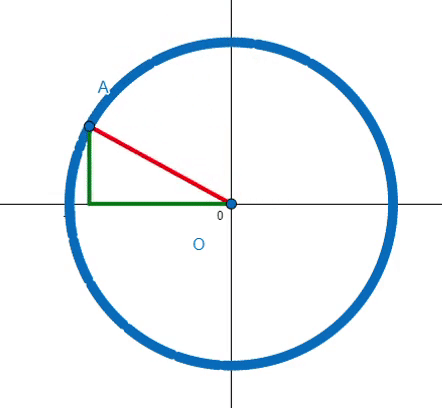
The animation below illustrates the transformation as b² transitions from 1 to -1, while a² remains at 1 throughout.

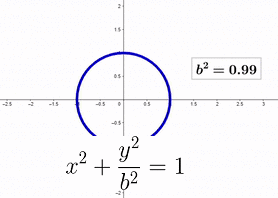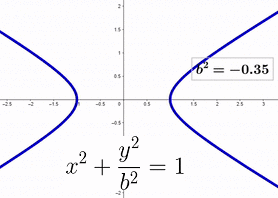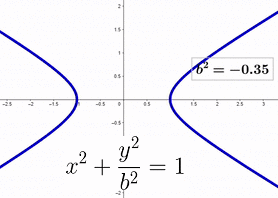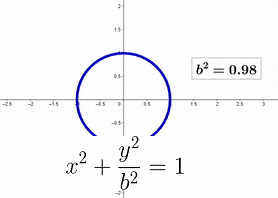
The shift from a circle to a unit parabola is smooth, except where b² = 0. Once b² becomes negative, b takes on an imaginary value. Consequently, a unit parabola can be viewed as a unit circle with the y component scaled by the imaginary unit i.

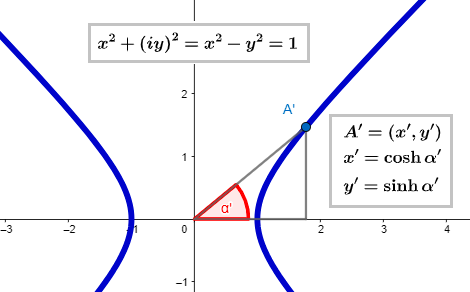
The parametric equations defining the hyperbola x² - y² = 1 relate to the hyperbolic sine and cosine, with the hyperbolic angle serving as their parameter. Unlike the circular angle, this hyperbolic angle is not associated with a length along the curve. Nonetheless, we can correlate it with twice the area defined by the curve, the x-axis, and the hypotenuse of the corresponding right triangle, similar to the circular angle.

Redefining Trigonometry through Exponential Functions

We can illustrate the algebraic relationship between circular and hyperbolic trigonometric functions by representing the circular functions using the exponential function.

Consider the polar and rectangular representations of complex numbers on the unit circle as a function of ?. From this basis, we can express the cosine function in terms of polar complex numbers.

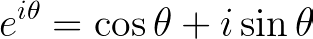
(If you find this concept unfamiliar, refer to our previous article on Euler’s Identity and the Roots of Unity.)

We can isolate the cosine function as follows:

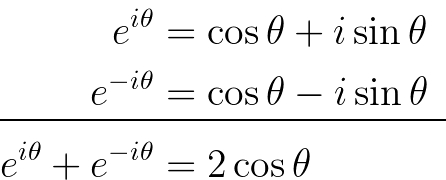
This gives us a formula for cosine:

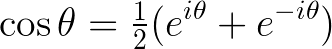
Similarly, we can derive the sine function through algebraic manipulation:

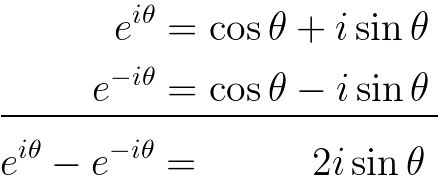
Thus:

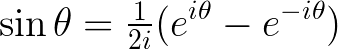
Visualizing the above relationships can be easier when represented as vectors, where their sums reflect the vector sums.

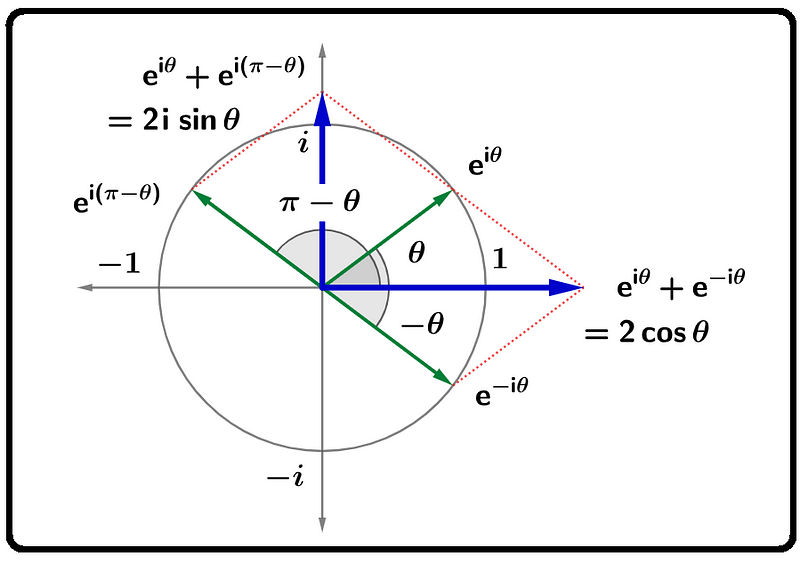
Here are the three main functions—sine, cosine, and tangent—represented as complex functions in polar form. The cosine function can be extracted with relative ease from the sum of two vectors, while the sine function requires a bit more effort:

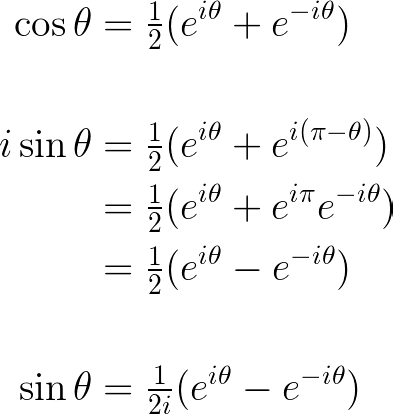
The tangent function, however, lacks the simplicity seen in sine and cosine.

The Role of the Imaginary

These exponential representations enable us to extend the domain of standard trigonometric functions into the realm of complex numbers. For instance:

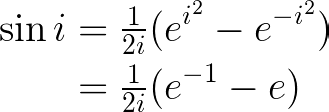
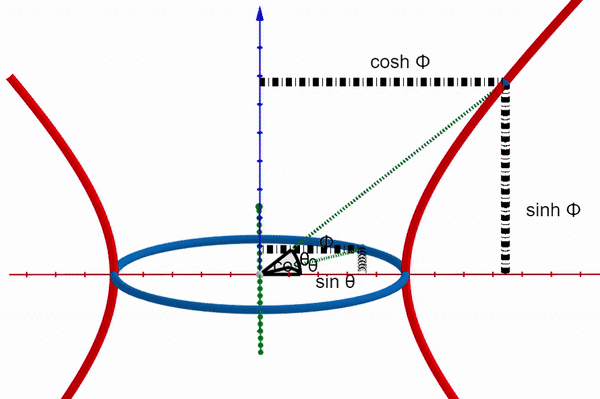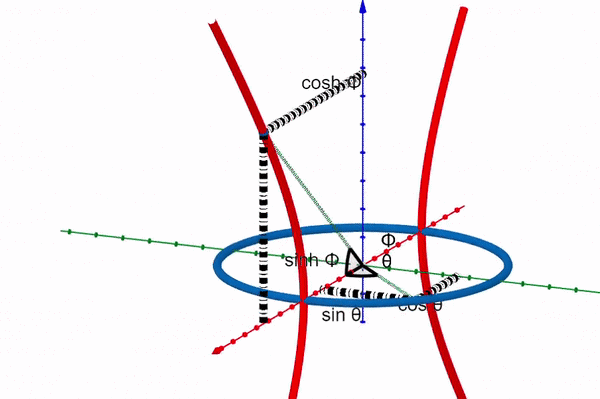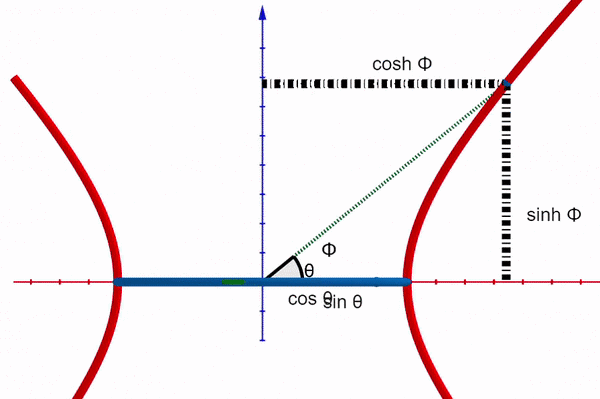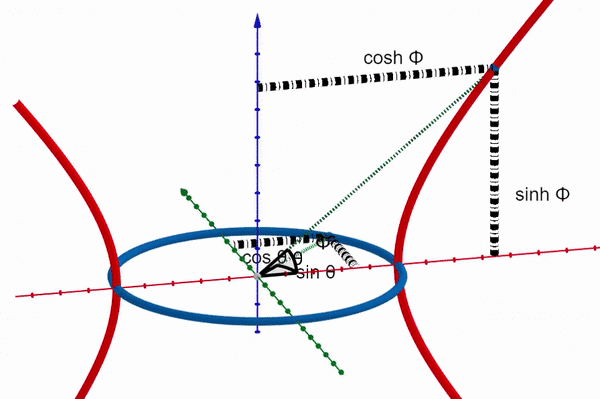
Returning to the idea that the hyperbolic angle serves as the imaginary counterpart of the circular angle, we typically assign the x-axis to the real component and the y-axis to the imaginary component when depicting complex numbers. Imagine placing two planes at right angles to each other.

In this representation, the x-axis corresponds to both the circular and hyperbolic cosine, with the real angle extending along the y-axis while the hyperbolic angle stretches along the z-axis.

Since the hyperbolic angle is the imaginary counterpart of the circular angle, we can establish a link between the two forms of trigonometry:

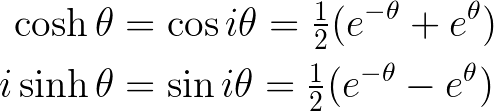
Recall that a circle represents the set of points equidistant from a center? We can modify the equation x² + y² = r² into a distance formula:

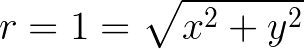
We can maintain this distance formula for the hyperbola but must express it as a hyperbolic distance, d. Thus, it still represents a collection of points with a shared hyperbolic distance from a center:

Like the Pythagorean identities for circular trigonometry, hyperbolic trigonometry has its own identities. Here’s one example:

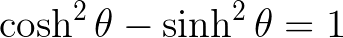
Now, we have introduced an imaginary z-axis. You may ponder the existence of an imaginary y-axis. To clarify, let’s revisit our circular distance formula:

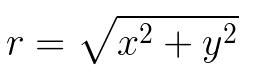
The modulus of a number indicates its distance from the Origin, extending the concept of absolute value beyond real numbers. If we consider r to represent the modulus of a complex number z = x + iy, it can be determined by the square root of the product of z and its conjugate:

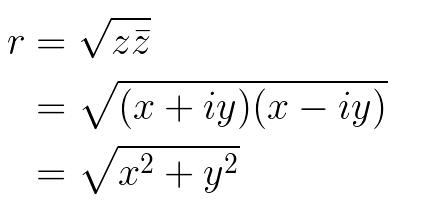
Next, let’s define a second imaginary number, u:

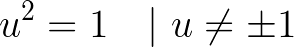
This additional imaginary number, u, signifies the set of hyperbolic or split complex numbers, which we will denote as w.

Returning to the previously defined distance formula for circular trigonometry, we can similarly define the hyperbolic distance, d:

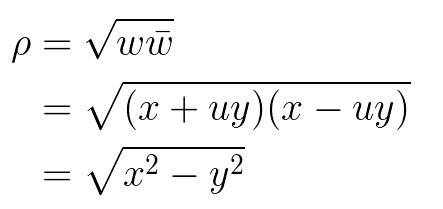
Those interested in special relativity might recognize a familiar concept: when x = 1, we derive the reciprocal of the gamma factor, and when y represents velocity as a fraction of light speed, the hyperbolic distance translates to the contracted length of a moving object.

What about the hyperbolic angle? We still need to demonstrate that this corresponds to twice the area between the hyperbolic radius and the hyperbola.

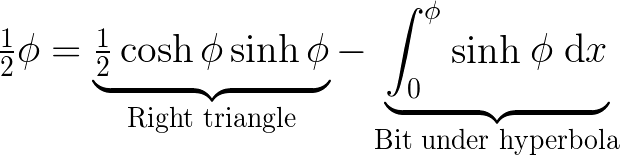
The first part of the formula represents the area of a triangle.

Area of the Triangle

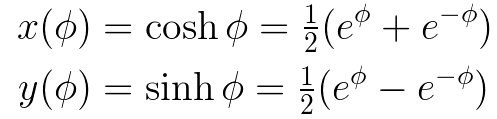
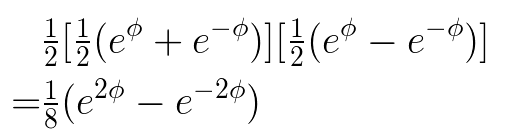
Area Under the Hyperbola

To finalize the integration, we require a conversion:

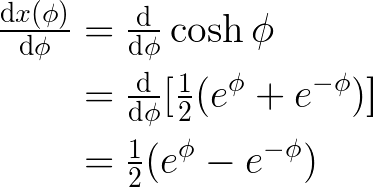
Now we can integrate, beginning by converting the integral:

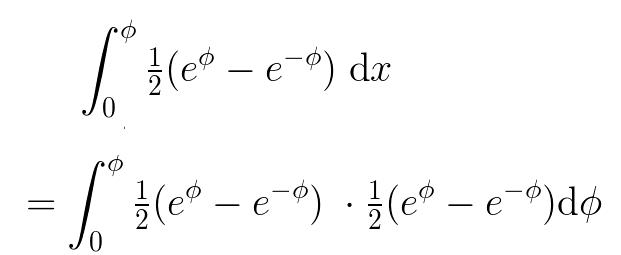
Next, we can work through it:

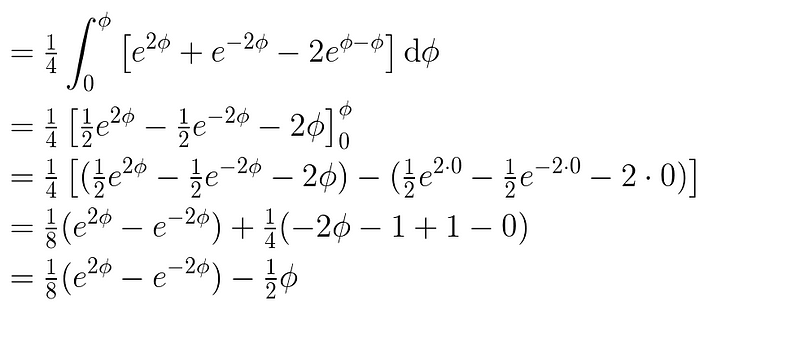
Finally, we subtract the area under the hyperbola from the area of the triangle:

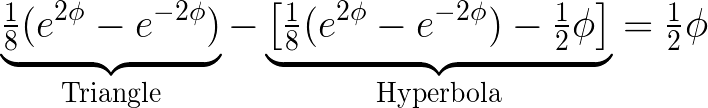
Isn’t it intriguing? You might find yourself wanting to delve deeper into this topic!

Postscript

In conclusion, let's revisit the infinite series representation for the exponential function.

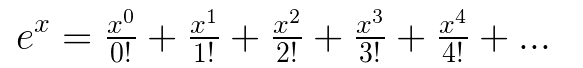
By leveraging this along with our exponential expressions, we can derive new series for trigonometric functions. Here’s an example:

This can be expressed more concisely as:

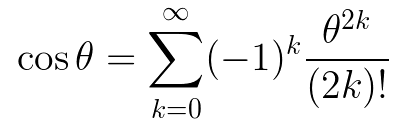
Feel free to attempt the same for the sine function and hyperbolic functions. If you're feeling adventurous, try creating your own trigonometric functions based on other conic sections.

Happy exploring!