Divide and Conquer

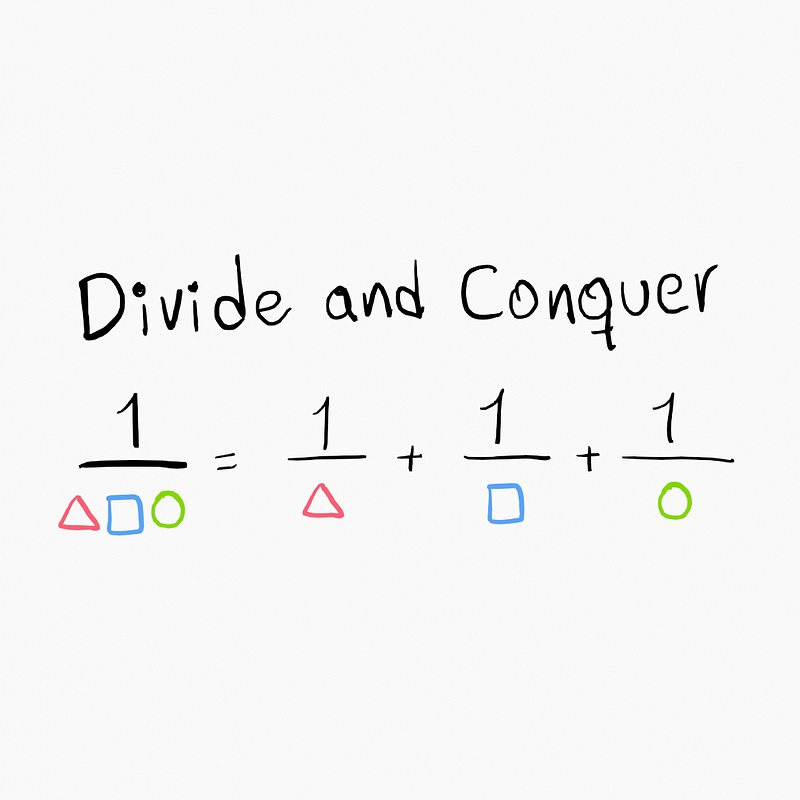
Partial fractions are a fascinating tool that simplifies intricate systems into manageable components, enabling us to grasp the complexities of the Mechanical World more intuitively. By mastering this concept, you'll gain a broader perspective on modeling reality.

This article aims to provide a holistic view of mathematics, physics, and engineering topics. Much like crossovers in cinema, I believe that understanding partial fraction generalization requires connecting it with other concepts.

Tackling Complex Systems

How do we approach intricate systems, such as societal structures or the human brain? The common solution is to "divide and conquer."

As humans, it's challenging to grasp a complex system in its entirety; we must break it down into smaller, comprehensible segments before reconstructing the overall complexity from these familiar building blocks.

Is this method solely a limitation of our cognitive abilities? Not at all; it mirrors the very fabric of Nature!

• Matter consists of particles.
• Interactions are governed by forces.
• The brain operates through neurons.
• Society is composed of individuals and subgroups.
• DNA is structured by genes.

Almost any complex concept can be deconstructed into simpler elements, making them easier to understand.

Modeling Reality with Fractions

When we use mathematics to model reality through functions, the "divide and conquer" principle is precisely what partial fractions accomplish. We can transform complex systems with multiple poles into simpler systems, each with a single pole.

But how do we represent the real world with functions?

The Language of the Mechanical Universe

How can we comprehend the universe to predict its future based on past and present knowledge?

In this analogy, systems function as the subjects while signals act as verbs. Systems are the tangible entities in reality, transmitting information and interacting with each other.

Signals

Most signals are time-based, although they aren't always limited to this.

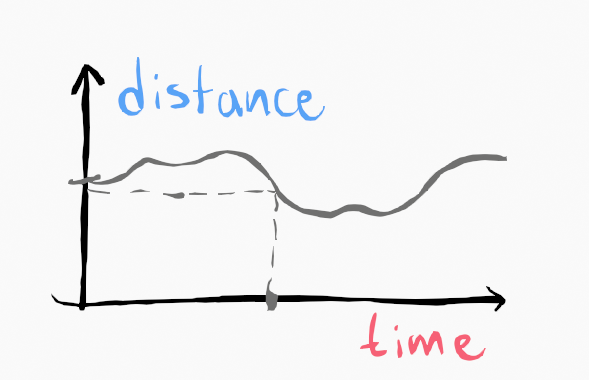
The graph can be represented as a function (e.g., through the Taylor series), which allows us to model a signal as a function comprising time-based values.

Systems

Systems are akin to cache-saved signals. While signals are intangible as they represent traveling information, systems are concrete objects occupying space, while signals are time-specific.

Mathematically, a system is the signal that produces the impulse response.

> Crossover: Through the concept of relativity, we perceive time and space as interconnected; thus, we model both systems and signals as functions.

> Another crossover: Systems align with matter (like quarks and leptons), while signals correlate with forces (such as bosons). This relationship can be observed through the standard model of particles within this context.

Additional Intuition

We can view complex systems as DNA, with genes serving as their fundamental components. The equations governing these systems are referred to as Characteristic equations, closely related to the concept of eigenvalues in linear algebra.

The terms ‘genes,’ ‘eigen,’ and ‘characteristics’ share a common etymological thread, representing the essence or intrinsic nature of something.

In engineering, the eigenvalues of a system's characteristic equation correspond to natural frequencies. You may have encountered the phrase "Everything has its own natural frequency," which, while it may sound mystical, holds significant physical meaning.

Thus, through partial fractions, we seek to identify the genes—the natural frequencies of the system's vibrations. Partial fractions enable us to isolate these natural frequencies for individual analysis.

Motivation for this Discussion

I recently encountered an intriguing image on X (Twitter) that encapsulates this generalization, which I'd like to share. (https://x.com/Psicoalfanista/status/1786087681509703873)

1. The first scenario occurs when poles do not repeat and have no power greater than one, merely appearing once.

Poles represent locations where division by zero occurs in control systems.

However, this first case does not explain how to determine the values of c_i.

2. The second scenario introduces a method for finding c_i by evaluating the Q(x) function at the pole's location.
3. The third instance involves a pole raised to a power greater than one. It's crucial to note that this method only applies when the exponent is a natural number (1, 2, 3, etc.), as it does not hold for real numbers outside the naturals.

Though this case seems straightforward, it remains incomplete. It fails to specify how to find c_{k,i}, the coefficients of the numerator.

4. The final case presents a more complex formula to resolve this, which can be challenging to grasp.

The Generalization

This generalization is insightful (once understood) and somewhat self-evident.

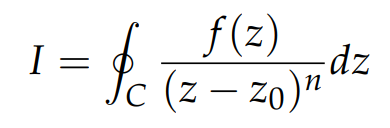
Spoiler Alert: This integral yields the residue, which is precisely what we seek when performing partial fractions.

Where does this integral originate from, and why do we utilize it for finding coefficients in partial fractions?

The answer lies in the Taylor series. To be more precise, it refers to the generalization of the Taylor series, known as the Laurent series.

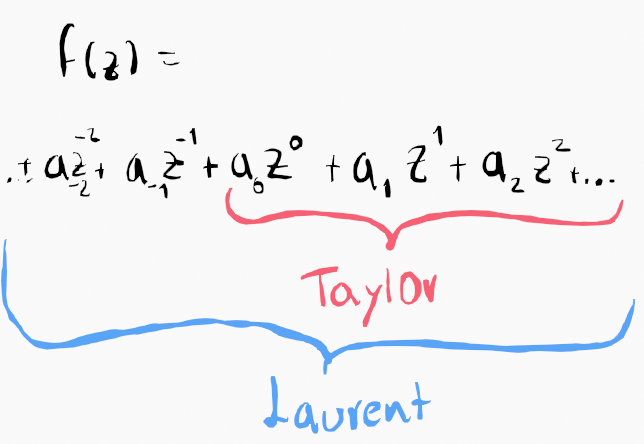
While the Taylor series aims to describe all analytical functions (continuous and differentiable), it falters in the presence of poles. The Laurent series addresses this limitation, functioning even when singularities, such as poles, occur.

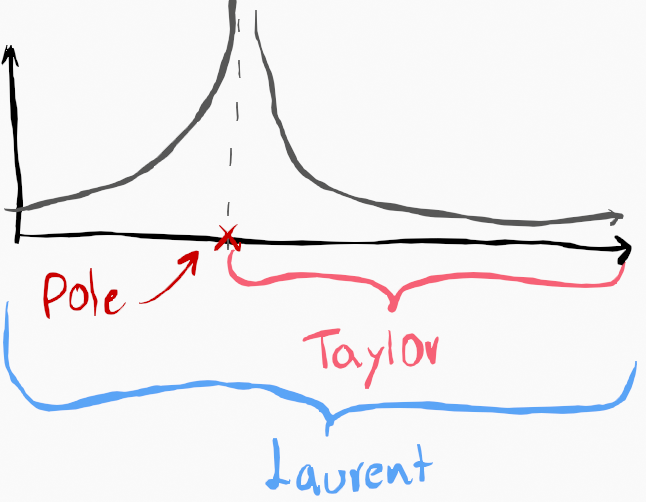
Since partial fractions involve multiple poles, the Taylor series isn't applicable. Remember that poles are singularities—locations where the function is undefined. The emergence of the Laurent series was a solution to this dilemma.

Spoiler Alert: The generalization entails decomposing the original fraction into its poles, which will lack a coefficient for each pole—the residue of the pole applied to the original fraction. This method is founded on the application of the Laurent series to the original fraction.

Another Crossover

The generalization of Cauchy’s integral formula aligns with the Generalized Stokes theorem.

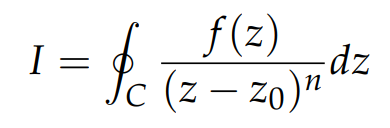
I have mentioned the solutions, but I will elaborate on why and how they connect with partial fractions.

But… Why and How

All four examples presented in the motivational image can be unified under a single generalization: Cauchy’s integral formula for calculating residues.

I've previously written about these concepts, particularly the initial case (the first two formulas in the Generalization pathway image):

<div class="link-block">

<div>

<div>

<h2>Math trick: Partial fraction decomposition (Case 1)</h2>

<div><h3>Discover a straightforward way of calculating partial fractions coefficients.</h3></div>

<div><p>medium.com</p></div>

</div>

<div>

</div>

</div>

</div>

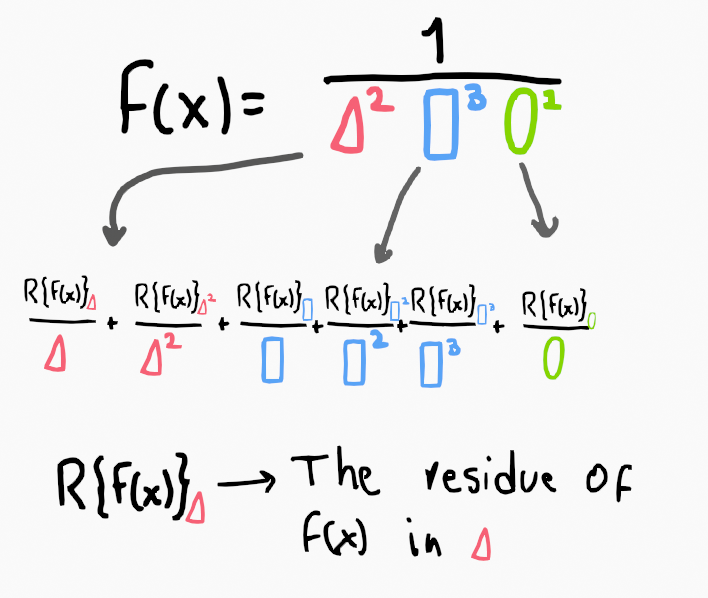
In summary, we simply separate the denominator's terms (note that the numerators/residues are omitted for illustration), as depicted in this image:

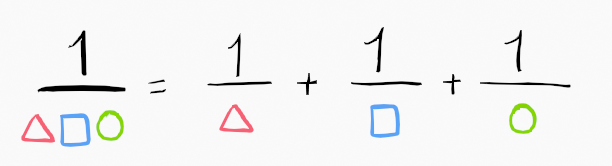
How do we determine the numerator for each term? They correspond to the respective residue of each pole, utilizing the Cauchy’s Residue Theorem.

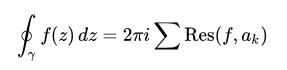
The previous section, "Math trick: Partial fraction decomposition (Case 1)," only addressed non-repeating poles. Since the generalization includes them, we should account for this.

In that discussion, we learned how to calculate the residue for distinct poles. Incorporating repeated poles requires applying derivatives for each instance of repetition, which is straightforward.

An example with numerical values:

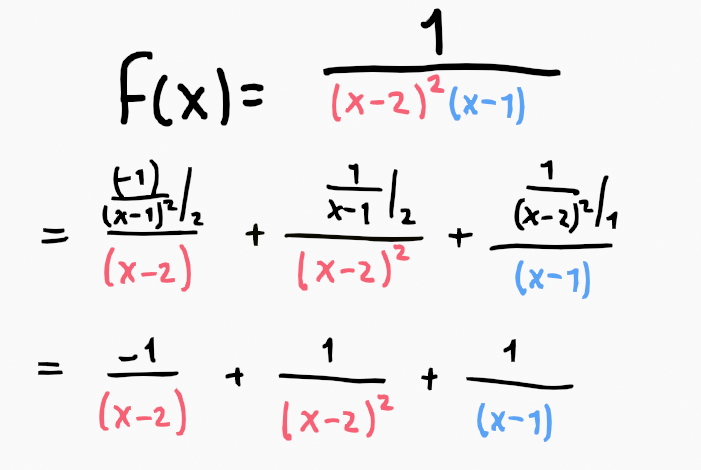
In conclusion, particles may be singularities (a hypothesis of mine), much like black holes (as proposed by Roger Penrose). The distinction lies in that black holes are singularities in space, while particles represent singularities over time. This doesn’t imply they trend toward infinity but rather indicates a state of "undetermined" values as they oscillate (though with a singular frequency).

This perspective leads me to assert that singularities possess unique identifiers based on their frequency and residue.

Here:

<div class="link-block">

<div>

<div>

<h2>det(A)=0 is not a problem anymore</h2>

<div><h3>We avoid facing singular matrices at all costs, but there is a way…</h3></div>

<div><p>medium.com</p></div>

</div>

<div>

</div>

</div>

</div>

How do we derive Cauchy’s integral formula?

This connection arises from its relationship with the Laurent series, which accommodates both positive and negative powers in its expansion. In the context of partial fractions, we primarily focus on the negative powers:

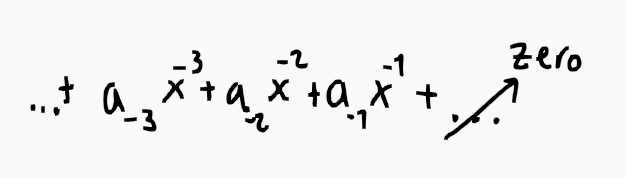
What if we want to apply the Laurent series to a function relevant for partial fractions? For instance, consider:

You might expect an infinite series of negative powers of x; however, this is only true if approached incorrectly (without utilizing the residue theorem for closed integrals). If you use the residue theorem wisely, you'll discover this forms the foundation of the generalization in partial fractions.

Initially, partial fractions were approached through various techniques that yielded results without necessarily understanding the underlying reasons (like the Heaviside method) or relying on template formulas for three cases to identify constants A, B, and C through extensive algebra.

How do we prove that the coefficient formula for Laurent’s series aligns with Cauchy’s integral formula? The demonstration is hinted at in The Language of the Mechanical Universe, but let’s examine the coefficients formula directly.

Just as Taylor's series employs a formula to find coefficients:

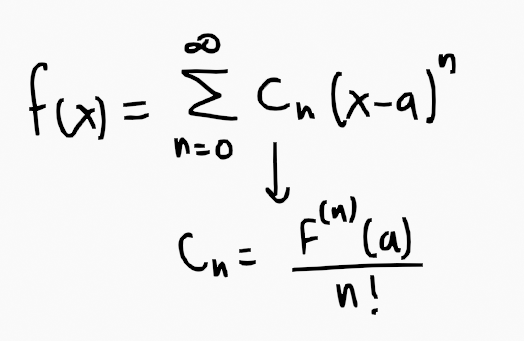
The formula for Laurent’s series is articulated as follows:

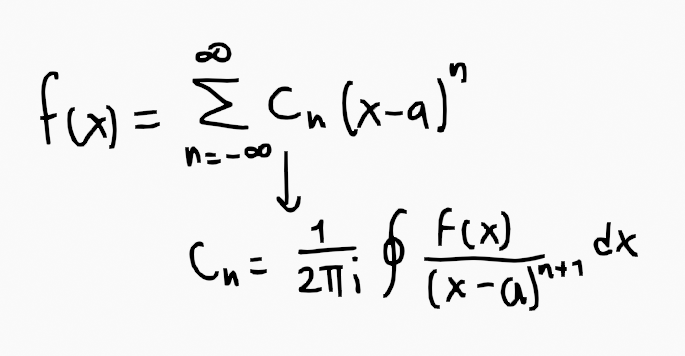
Upon close examination, you will realize that it mirrors the Cauchy’s integral formula previously discussed.

The (2*pi*i) in the denominator cancels with the (2*pi*i) derived from the residue theorem, as each residue contains a (2*pi*i) term. While it's not technically correct to omit it, I occasionally do (as have others). The reason for the occasional presence of ‘n’ instead of ‘n-1’ relates to our specific context, where negative powers are prioritized over positive ones. We can reformulate the term to adjust ‘n’ from 1 to infinity, where 1 denotes the first negative root or pole. Ultimately, they yield the same results.

Summary with an Example

The generalization of partial fractions involves decomposing into each root independently, complete with its corresponding pole residue.

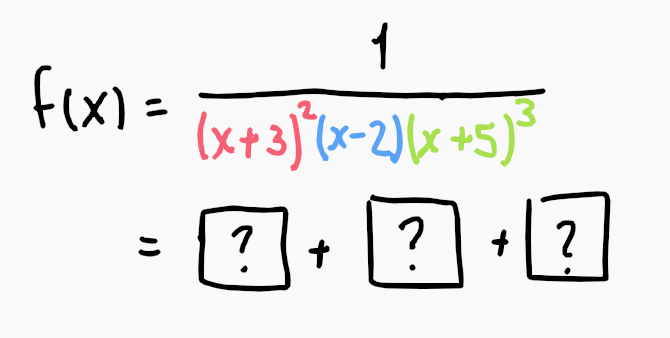
Let’s break this down into two stages:

1. We isolate the poles into distinct fractions, summing them accordingly.
2. We determine the numerator's value for each fraction.

The first stage encompasses individual division by roots. If they repeat, we factor in their successive powers until we replicate the original power.

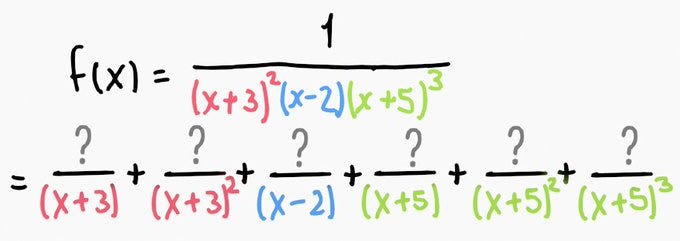
Once we've successfully separated the terms into distinct addends, we proceed to the second stage.

In this stage, we calculate the numerator for each term.

The Cauchy residue theorem states that when we divide by a pole, an associated residue exists. The numerator we need to find corresponds to the residue of its respective pole in relation to the original fraction.

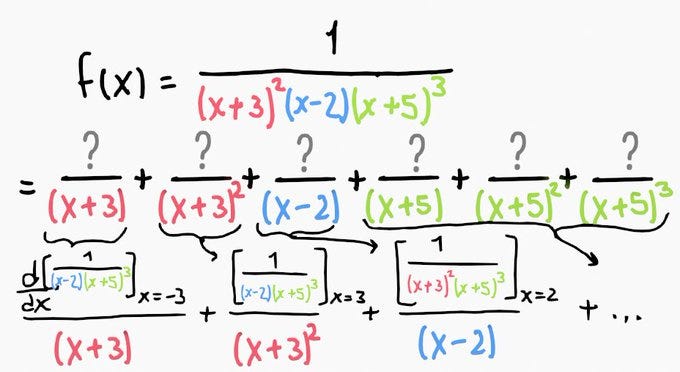
The residue at a pole is determined by evaluating the original fraction at the pole's location while omitting the denominator's pole. This approach slightly alters when dealing with repeated poles, in which case we differentiate n times before evaluation.

For instance, the residue of f(x) for the pole 1/(x-2) would involve evaluating 1/(x+3)²(x+5)³ at x=2.

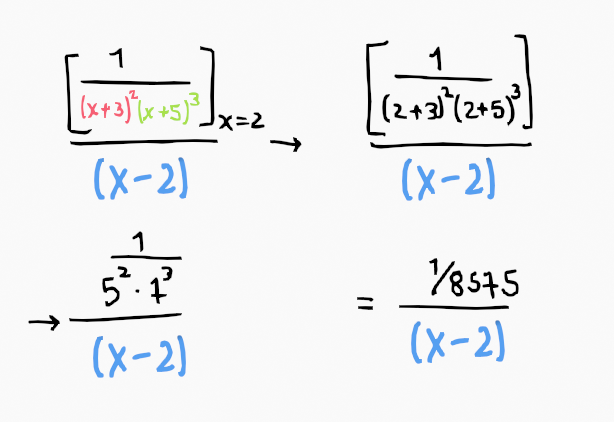
When dealing with a repeated pole, we apply the derivative, which adjusts the power of the pole downwards.

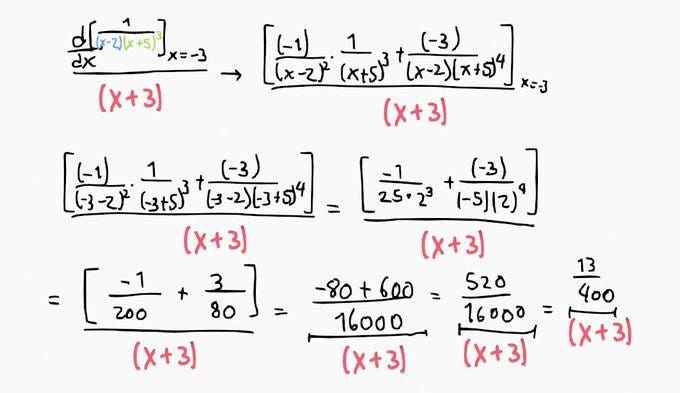
We can verify the previous results with an external tool:

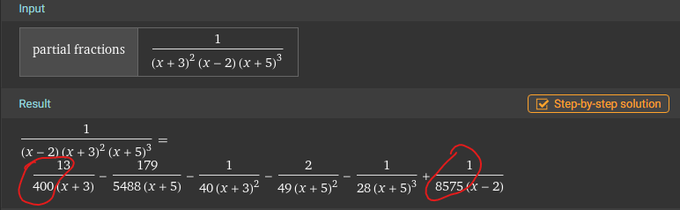
Note

I must emphasize that singularities are of paramount importance. I have even suggested that particles are singularities (a theory based on my extensive research). If you're interested in uncovering the "theory of everything," I recommend starting to view all entities as singularities (including black holes, the initial moment of the Big Bang, particles, and the current Universe's horizon). From my perspective, they form the foundational elements of reality.

I have attempted to develop a theory of everything that integrates mathematics with a final theory of numbers, leading to intriguing discoveries about transfinite numbers. I may not complete this endeavor due to a lack of motivation, as it demands considerable time and energy. Additionally, I would need to navigate data from other theoretical frameworks, requiring me to learn advanced concepts, which I find exhausting. I have amassed over 800 pages of notes that I am reluctant to revisit, some of which are chaotic and incomprehensible.

However, I have decided to share my personal notes and significant insights from these attempts, even though many are still in a rough state. I aim to demonstrate the more challenging assertions, even if I might be mistaken in some aspects.

It's likely more beneficial to share my ideas in a structured manner here rather than continue accumulating handwritten notes that I will not revisit. I plan to share various concepts over time, even those that I initially hesitated to present until I felt they were complete.

Thank you for reading.

Next Story: I suspect that the current definition of energy is flawed, which has led Einstein to propose an energy formula that falters at the quantum level. This matter relates to perspective. While Einstein's viewpoint is valid within a certain context, there exists another perspective that could offer a better understanding. I will not delve into this topic in detail here; I will merely introduce it, motivated by a meme. This subject is extensive, so I will only provide a brief introduction. The new energy definition could lead to significant shifts in physics formulation, as it challenges the definition rooted solely in a spatial framework. The key is to consider space-time as a unified whole for this new definition of energy.

This writing style is somewhat reminiscent of "Rayuela," as I have introduced various concepts and spoilers that I did not elaborate on, as they will be interrelated with future writings. As you may notice, I connect each new discussion with previously established concepts. Crossover?