The Genius of Lewis Fry Richardson: A Legacy of Humanity and Science
Written on
Lewis Fry Richardson: A Polymath Driven by Humanitarian Concerns
“Big whirls have little whirls that feed on their velocity, and little whirls have lesser whirls and so on to viscosity.” — Lewis Fry Richardson (1881–1953)
My initial exposure to the contributions of Lewis Fry Richardson came through my friend and collaborator, John Knox. In 1998 and 1999, we released two papers detailing innovative closed-form methods for approximating the base of the natural logarithm. During that period, the calculation of e garnered more attention, and mathematicians were likely more familiar with its formulas. Consequently, neither the editors nor the reviewers noticed that one of our so-called new methods, known as the Mirror Image Method (MIM), had actually been introduced in a 1927 paper titled “The Deferred Approach to the Limit,” co-written by Richardson.
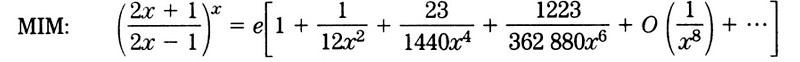
John, a meteorologist, shared with me that Richardson was one of his heroes, and he felt no shame in having his work overshadowed by such a figure.
As I delved deeper, I understood why John revered Richardson so highly. L. F. Richardson was an exceptionally talented, accomplished, and empathetic individual. His mathematical innovations found applications across various fields, making it challenging to categorize his achievements simply.
Meteorology
In the field of meteorology, Richardson was truly ahead of his time. When weather prediction relied heavily on intuition and experience, he introduced the idea of employing mathematical equations for forecasting. His 1922 book, Weather Prediction by Numerical Process, laid the groundwork for contemporary computational forecasting.
Richardson’s methodology involved using finite differences to solve differential equations, which he applied to atmospheric dynamics. He divided the atmosphere into a grid, utilizing his equations to represent each segment and aiming to predict weather changes based on the interactions within these segments.
You might think, “That sounds reasonable.” However, consider that one of the differential equations he worked with, the horizontal momentum equation, is quite complex:
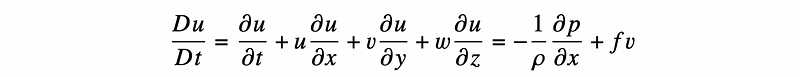
In this equation:
- Du/Dt indicates the total change in u, the x-directional component of velocity, over time.
- ?u/?t signifies the partial derivative of u concerning t.
- u(?u/?x), u(?u/?y), and u(?u/?z) represent advection of u in the x, y, and z directions. According to NOAA, advection involves the “transport of an atmospheric property by the wind.”
- ? denotes air density.
- p indicates pressure.
- (-1/?)(?p/?x) quantifies the pressure gradient force per unit mass in the x direction, illustrating that air moves from high-pressure regions to low-pressure ones.
- f is the Coriolis parameter, and
- v represents the velocity component in the y direction.
The complexity of such calculations highlights a significant limitation of his insightful approach: the extensive time required to generate forecasts. Richardson estimated that about 60,000 individuals with slide rules would be needed to predict the weather for just one day. This number equates to equipping the entire population of a city like Cupertino, CA, or Chapel Hill, NC, with slide rules! To become viable, Richardson’s forecasting methods had to await the invention of computers post-World War II.
Mathematics
Through his exploration of weather prediction and fluid dynamics, Richardson devised mathematical tools with broad applicability.
One of his notable contributions is the Richardson number, Ri, which serves as a rough gauge of whether fluid flow remains stable or is likely to become turbulent. Essentially, it assesses the propensity of a stratified fluid to resist mixing.
Buoyancy tends to stabilize fluid flow, while shear (the change in horizontal velocity concerning height) destabilizes it. The Richardson number therefore compares these two effects:
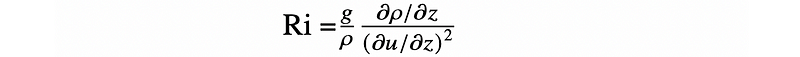
In this equation, z is the vertical coordinate, u is the fluid's velocity, and ? is the fluid's density.
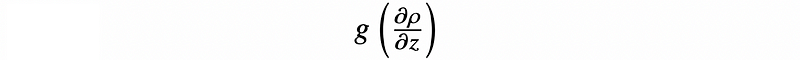
This equation illustrates the stabilizing effect of buoyancy (with g representing the acceleration due to gravity), while
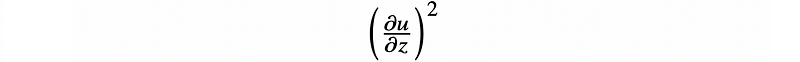
This equation represents the destabilizing influence of velocity gradients (shear).
When Ri > 1, buoyancy predominates, leading to stable fluid flow. Conversely, when Ri < 0.25, shear forces dominate, suggesting that the fluid is likely to become turbulent. Values in between indicate a transitional zone of moderate stability.
The Richardson number is widely utilized in atmospheric stability studies, oceanography, and aviation turbulence forecasting.
Richardson also developed noteworthy techniques like Richardson extrapolation and Richardson iteration. The former enhances the accuracy of numerical approximations by using varying step sizes to cancel out significant error terms. The latter helps solve systems of linear equations in the form A**x = **b, where A is a matrix, x is an unknown vector, and b is the resultant vector. These numerical methods warrant their own detailed discussions—if readers express interest, I am happy to write separate articles on them.
One of Richardson's most relevant explorations to my work is his analysis of the coastline paradox. He noted that, unlike familiar geometric shapes (e.g., triangles or squares), the length of any given coastline depends on the measuring instrument's length. Specifically, he found that the border between Spain and Portugal was measured as 987 km by Spain but as 1,214 km by Portugal—a 23% discrepancy. He observed that as the measuring tool's size decreased, the coastline length increased.
As peculiar as this might sound, Richardson's observations and analyses led Benoit Mandelbrot to recognize this phenomenon as an example of fractal scaling in nature, subsequently leading to the development of the essential box-counting method for assessing fractal scaling in images.
Pacifism
Lastly, Richardson was a dedicated humanist. His deep concern for the well-being of others was, by many accounts, the driving force behind his relentless quest to understand the natural processes impacting humanity's quality of life.
Raised in a Quaker family as the youngest of seven children, Richardson embraced the concept of social justice as a core value and became a pacifist early in his education. When World War I erupted, he was employed at the Meteorology Office at the National Physics Laboratory. He declared himself a conscientious objector and, in service to his country, chose to drive for the Friends Ambulance service.
The horrors of war profoundly affected him. He began applying his mathematical expertise to analyze and comprehend the root causes of conflict, investigating the dynamics of arms races, territorial disputes, and the probability of war. In 1935, he published Mathematical Psychology of War, introducing what is now known as the Richardson arms race model. This model utilized differential equations to illustrate how one country's arms expenditures could influence another's, attempting to quantify the idea that mutual fear and the quest for security could lead to escalating armament and potential warfare.
Ironically, this very research inspired him to discover the previously mentioned coastline paradox by examining how shared territorial borders influence conflict likelihood.
In 1969, in recognition of his groundbreaking contributions to the field, Lancaster University established the Richardson Institute, dedicated to the study of peace and conflict resolution.
Final Thoughts
To me, L. F. Richardson epitomizes the heights of human achievement. Throughout his life, he served as a mathematician, chemist, physicist, meteorologist, and even an ambulance driver. His endeavors appeared to be fueled by a profound desire to create a better and safer world for everyone.
As often occurs with true visionaries, Richardson did not live to see the full impact of his work. He passed away in 1953, just a year before the BBC aired its inaugural weather forecast.
Thank you for reading! If you enjoyed this piece, please feel free to hit the “Applause” icon at the top as many times as you’d like. You can also subscribe to receive my latest content directly in your inbox.
Further Reading
Lewis Fry Richardson - Biography
Lewis Fry Richardson was an English mathematician, physicist, and meteorologist who pioneered modern mathematical...
mathshistory.st-andrews.ac.uk
Lewis Fry Richardson - A Pioneer Not Forgotten
Lewis F Richardson, a physicist by training, remains a towering presence in two academic subjects, meteorology and...
link.springer.com