Exploring the Depths of Fractal Geometry: A Journey Through Time
Written on

Fractal geometry captivates us with its intricate patterns and the elegance found in nature's irregularities. Whether it's the fluidity of waves or the asymmetric symmetry of leaves, humans inherently seek patterns. These patterns help us assess our surroundings, especially regarding potential dangers. In ancient hunter-gatherer societies, any disruption in routine was a signal that something was amiss. Patterns also play a crucial role in our biology, as most processes are repetitive, leading to visual representations of distinct forms.
In mathematics, fractal geometry is the branch dedicated to exploring continuous, patterned yet irregular scalar symmetries.

The roots of modern fractals can be traced back to the 17th century when René Descartes introduced the concept of graphing polynomial functions. Although these functions were groundbreaking, they failed to effectively depict the patterns observed in reality. The mathematical community recognized this limitation, as complex polynomials were cumbersome and did not accurately illustrate organic patterns.
A paradigm shift was necessary: instead of merely analyzing the patterns themselves, mathematicians needed to understand the iterative processes that produced them. Nature is inherently generative, shaped by evolutionary forces that optimize processes, exemplified by the Fibonacci sequence seen in sunflowers and spiral shells. This sequence, while simple, illustrates the power of iteration, where each new number is derived from the sum of the two preceding ones.
Fractals are complex, infinitely detailed patterns that exhibit self-similarity at various scales. They arise from recursive functions within complex spaces, enabling us to replicate the irregularities found in the world around us.
Before delving into the contributions of Gaston Julia, it’s essential to understand complex functions.
Quick Prerequisite
A complex number consists of two parts: a real and an imaginary component, represented as a + bi. In practical applications, these complex numbers are often denoted simply as z.
Complex Numbers & Polynomials
Complex numbers are graphed on a unique coordinate system known as the complex plane, which includes both real and imaginary axes.
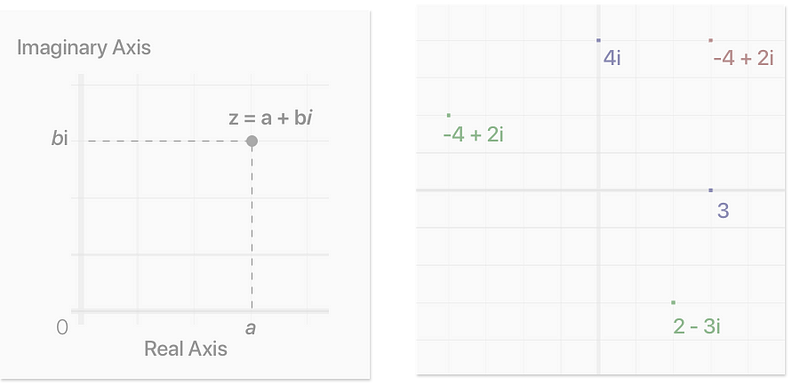
The complex plane deviates from the traditional Cartesian system, aligning instead with the real and imaginary axes. Graphing complex numbers becomes straightforward once they are separated into their components.
Magnitude of Complex Numbers
Like natural numbers, complex numbers possess a magnitude, or "size." However, determining the magnitude of a complex number involves more than just identifying its absolute value:
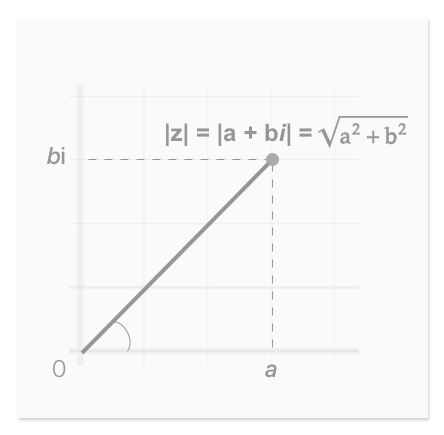
Using the Pythagorean theorem, the magnitude of a complex number is defined as the shortest distance from the point to the origin in the complex plane.
Under Iteration, Limits & Orbits
The behavior of fractal geometry arises from iterating complex functions, particularly z² + c. The key focus is on magnitude; similar to determining limits of natural functions as X approaches infinity, fractals explore whether a complex function's orbit escapes from the origin, indicating that its magnitude approaches infinity during iteration.
Prequel — Gaston Julia
The journey of modern fractal geometry began in the early 1900s with Gaston Julia, a young student deeply intrigued by the interplay of music and mathematics, particularly within the realm of complex numbers and functions.

Julia's pivotal work was inspired by Sir Arthur Cayley's 1879 paper, The Newton-Fourier Imaginary Problem, where Cayley sought to find roots of the equation f(z) = z³ + c = 0 through the Newton-Raphson method. He posed a challenge: could the roots be predicted based on initial values of z? Although he made strides in exploring "basins of attraction" through iteration, the limitations of technology at the time hindered a complete understanding of these complex shapes.
Unfortunately, Gaston’s academic pursuits were interrupted by World War I, where he suffered severe injuries. Nevertheless, upon his return, he focused on complex polynomial functions and published a significant 199-page memoir titled Mémoire sur l’itération des fonctions rationnelles in 1918, which won the prestigious Grand Prix from the French Academy of Sciences. This publication laid the groundwork for what we now recognize as fractal geometry, alongside contributions from Pierre Fatou.
Julia Sets
Julia's dissertation explored the distinction between iterations of points that converge to a repeating pattern and those that escape to infinity. The patterns that repeat are known as Julia Sets, while those that escape correspond to Fatou Sets. The fundamental formula revolves around a complex binomial with a constantly changing element.
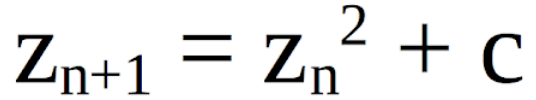
The Julia sets visualized below were generated using modern computational methods, demonstrating the complexity that Gaston Julia envisioned through his theoretical work.
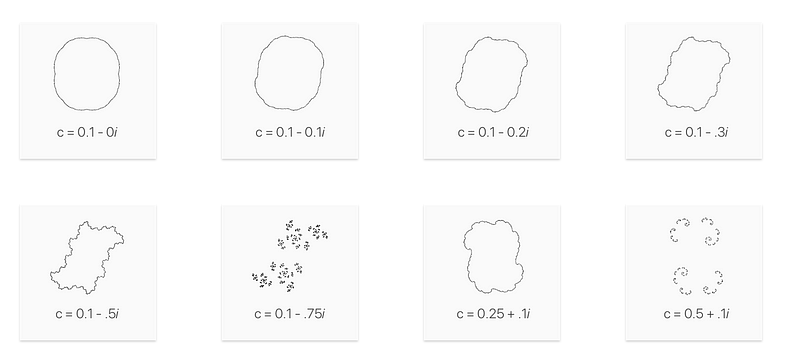
These visuals represent just a fraction of the vast variations possible within the complex plane. It’s intriguing to consider what might emerge if we iterated every point in search of Fatou and Julia sets.
Enter The Fractalist — Benoit Mandelbrot
After decades of stagnation, the term fractals gained prominence in the 1970s, thanks to Benoit Mandelbrot, who revitalized interest in the field.
Mandelbrot's journey began with an exploration of nature, culminating in his 1975 paper, How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. He analyzed the complexities of geographical curves and discovered their statistical self-similarity, where each part resembles a reduced-scale version of the whole.
Mandelbrot, born in Poland in 1924, had been influenced by both Julia's work and the study of complex functions. His groundbreaking research involved mapping Julia sets across the complex plane, marking points as white or black depending on whether they converged to a Julia or Fatou set.
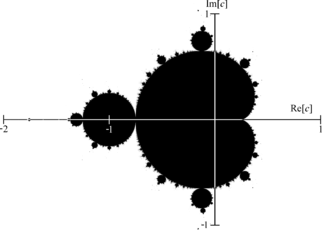
The resulting diagram became known as the Mandelbrot Set. While modern iterations feature vibrant colors, the original was a monochrome depiction. Mathematically, the Mandelbrot set comprises points in the complex plane where the corresponding Julia set remains connected. In essence, the Mandelbrot set serves as a comprehensive reference for all Julia sets.

This image encapsulates the essence of fractal geometry, illustrating the connection between the Mandelbrot Set and its corresponding Julia Sets. Each black point signifies a continuous Julia set, while the red point represents a Fatou set.
In Closing
Mandelbrot's dissemination of the Mandelbrot Set through various media elevated him to academic prominence, much like Julia's earlier contributions. This resurgence ignited interest in fractal geometry and laid the groundwork for new mathematical domains such as chaos theory.
It is a poetic irony that the exploration of imaginary numbers allowed us to understand the underlying order within chaotic systems. As both Julia and Mandelbrot demonstrated, a simple shift in perspective can unveil profound truths. This exploration is merely the beginning, as we shall soon venture into the significance of the Mandelbrot Set in three dimensions...